электродинамика
Как создается электрическое поле в проводнике с током?
Мотивация
Вопрос, вынесенный в заголовок, в свое время породил большую дискуссию на физическом форуме (1, 2, 3). Вот более точная формулировка вопроса:
Рассмотрим длинный провод, подключенный к батарейке. По нему течет постоянный ток. Ток создается электрическим полем Е, которое, в свою очередь, создается зарядами на полюсах батарейки. Почему вдали от полюсов (например, в середине проводника) поле Е=const, а не убывает при удалении от полюсов, как ему положено по закону Кулона?
Правильный ответ заключается в том, что батарейка не является единственным источником электрического поля, какие бы процессы в ней ни происходили. На поверхности проводника с током возникают дополнительные заряды, которые и создают постоянное электрическое поле внутри.
Обоснование появления зарядов на поверхности проводника с током следующее. Плотность тока внутри проводника по закону Ома пропорциональна напряженности поля:
$$\vec{j}=\lambda \vec{E}.$$
Возьмем дивергенцию обеих частей и воспользуемся первым уравнением Максвелла $$\text{div}\vec{E}=4\pi\rho$$ и законом сохранения электрического заряда в локальной форме $$\text{div}\vec{j}=-\partial\rho/\partial t$$:
$$-{\partial\rho\over\partial t}=4\pi\lambda\rho.$$(1)
Так как протекание тока — стационарный процесс, в котором величины со временем не меняются, то производная в левой части зануляется, поэтому правая часть — плотность зарядов внутри проводника — тоже есть 0. Следовательно, поле в проводнике может создаваться только зарядами на его поверхности.
В этом посте попробуем найти, каким именно должно быть распределение поверхностного заряда, чтобы внутри проводника с постоянным сечением создалось однородное электрическое поле.
Близкая задача из электростатики
К сожалению, мы не можем найти точное распределение поверхностных зарядов по проводнику, если не учтем механизм того, как именно создается разность потенциалов на его концах. Вместо выбора такого механизма сделаем приближение, сказав что никакого механизма нет. Фактически, будем решать упрощенную задачу: как нужно распределить заряд по поверхности, чтобы поле внутри стало таким же, как и при стационарном протекании тока?
Разумеется, распределенный по поверхности проводника заряд без механизма создания разности потенциалов сразу же растечется (характерное время растекания можно найти из уравнения (1)), и, казалось бы, решать такую задачу бессмысленно. Но можно сформулировать задачу из электростатики о проводнике во внешнем однородном электрическом поле с точно таким же ответом:
Цилиндрический проводник длины l и радиуса R помещен во внешнее электрическое поле, так что его ось направлена по полю. Найти распределение поверхностных зарядов.
Действительно, в этом случае заряды так распределятся по поверхности проводника, что линейный потенциал внешнего поля $$\varphi_\text{внеш}=-|E|x$$ будет скомпенсирован их собственным потенциалом $$\varphi=kx$$ во всем объеме проводника.
Для полноты отметим, что аналогичная задача проводнике сферической формы имеет простое точное решение.
Наивный подход
$$ \newcommand{\drawCircle}[3]{ \draw (#1,#2) arc (90:270:#3 and #2); \draw[dashed] (#1,-#2) arc (-90:90:#3 and #2); } \newcommand{\drawTik}[2]{\draw (#1,0.1) -- ++ (0,-0.2) node[fill=white,below,inner sep=0,pos=1.4] {$#2$}} \begin{tikzpicture}[>=latex] \def\rx{4} \def\xx{-1.9} \def\x{1.9} \def\ry{1.2} \def\e{0.48} \node[above right,inner sep=2] at (0,\ry) {$R$} \node[below right,inner sep=2] at (0,-\ry) {$-R$} \node[below right] at (0,0) {$0$} \draw[->,very thin] (-\rx-1,0) -- (\rx+1,0) node[below] {$x$}; \draw[->,very thin] (0,-1.5*\ry) -- (0,2*\ry) node[left] {$r$}; \draw (\rx,0) ellipse (0.48 and \ry); \draw[] (-\rx,-\ry) -- (\rx,-\ry) (-\rx,\ry) -- (\rx,\ry); \drawCircle{-\rx}{\ry}{\e} \drawCircle{\xx-0.1}{\ry}{\e} \drawCircle{\xx+0.1}{\ry}{\e} \node[above] at (\xx,\ry) {$dx_1$} \drawTik{\xx}{x_1} \drawTik{\x}{x} \draw[dashed](\xx,\ry) -- (\x,0) \draw (\rx,0) ellipse (0.25 and 0.62); \draw (\rx,0) ellipse (0.3 and 0.75); \drawTik{-\rx}{-{l\over2}} \drawTik{\rx}{l\over2} \draw[dashed] (\x,0) -- (\rx,0.68) node[inner sep=2,pin={[pin distance=6, pin edge={<-,solid,black},fill=white,inner sep=1]30:$dr$}] {} \draw[->] (2.8,\ry+0.8) -- ++(2,0) node[pos=0.9,above] {$\vec{E}$}; \end{tikzpicture} $$
Обозначим плотность зарядов через $$\sigma_1(x)$$ на боковой поверхности и $$\sigma_2(r)$$ на поверхности оснований. Через эти величины можно выразить электрическое поле или потенциал внутри цилиндра, взяв интегралы по поверхности. Скажем, на оси цилиндра
$$\varphi(x)=\int\limits_{-l/2}^{l/2}{2\pi R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}+ \int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r) \over\sqrt{r^2+\left(x-{l\over2}\right)^2}} -\int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r)\over\sqrt{r^2+\left(x+{l\over2}\right)^2}} =Ex.$$(2)
Здесь учтены симметрии задачи: вращательная симметрия вокруг оси повлияла на выбор элементов площади, а зеркальная симметрия выражается в том, что плотности зарядов на основаниях цилиндра имеют противоположный знак ($$\sigma_2$$ и $$-\sigma_2$$), и в том, что функция $$\sigma_1(x)$$ — нечетная.
Мы получили интегральное уравнение на $$\sigma_1(x)$$ и $$\sigma_2(r)$$. Я не смог решить его в явном виде. Можно было бы рассмотреть предельный режим, когда $$l\gg R$$, и поискать приближенное решение в области $$|x|\ll l$$. Тогда вкладом двух последних интегралов можно пренебречь, а в первом интегрировать от минус бесконечности до бесконечности:
$$\int\limits_{-\infty}^{\infty}{R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}=x.$$(3)
Здесь я опустил коэффициент пропорциональности, не влияющий на дальнейшие рассуждения. Это интегральное уравнение имеет вид свертки ядра $$k(x)=1/\sqrt{1+x^2/R^2}$$ и искомой функции. Такое уравнение можно решить, взяв преобразование Фурье от обеих частей:
$${\cal F}(\sigma_1)\int {e^{-ikx}\over\sqrt{1+\dfrac{x^2}{R^2}}}dx=\int xe^{-ikx}dx.$$
Интегрирование по частям справа дает $$\inline\int xe^{-ikx}dx=-i\delta(k)/k$$. Искомая функция ищется через обратное преобразование Фурье:
$$\sigma_1(x)={-i\over2\pi}\int\dfrac{\delta(k)e^{ikx} dk}{k\int {e^{-iks}\over\sqrt{1+\frac{s^2}{R^2}}}ds}.$$
Пока оставим попытки решить интегральное уравнение и посмотрим, что нам предлагает математика, а именно раздел, изучающий уравнения математической физики.
Аналитические методы заводят в тупик
Наша задача на языке математики формулируется так. Вне цилиндра потенциал подчиняется уравнению Лапласа $$\Delta\varphi=0$$ и стремится к нулю (как поле диполя) на бесконечности. На поверхности цилиндра потенциал фиксирован и описывается начальными условиями
$$\begin{align*}\varphi(x, R)&=Ex,\quad x\in\left[-{l\over2},{l\over2}\right],\\ \varphi\left(\pm{l\over2}, r\right)&=\pm E{l\over2},\quad r\in\left[0,R].\end{align*}$$
Это формулировка задачи Дирихле для уравнения Лапласа. Решение у этой задачи существует и оно единственно. Потенциал определяет электрическое поле вне цилиндра, а скачок нормальной составляющей электрического поля на границе цилиндра пропорционален искомой поверхностной плотности заряда.
Уравнение Лапласа в цилиндрических координатах с учетом цилиндрической симметрии задачи записывается так:
$${1\over r}{\partial\over\partial r}\left(r{\partial\varphi\over\partial r}\right)+{\partial^2\varphi\over\partial x^2}=0.$$(4)
Стандартный метод решения таких уравнений — метод разделения переменных, он же метод Фурье. Искомая функция ищется в виде суммы (конечной, счетной или интеграла) произведений функций, в которых каждый сомножитель зависит только от своей переменной:
$$\varphi(x,r)=\Sigma_kX_k(x)R_k(r).$$
Мы хотим, чтобы (4) выполнялось не только для всей суммы целиком, но и для каждого элемента $$X_k(x)R_k(r)$$. Подставляем его в (4) и получаем:
$${1\over rR_k}{\partial\over\partial r}(rR_k')=-{1\over X_k}X_k''=-\lambda_k.$$
После такой подстановки получилось представить равенство так, что левая его часть зависит только от координаты r, а правая — только от координаты x. Равенство возможно, только если никакой зависимости нет, то есть и правая, и левая часть равны некоторой константе $$\lambda_k$$. Дальше, в зависимости от вида граничных условий, выбирается одно из двух получившихся дифференциальных уравнений
$$\left\{ \begin{array}{l} R_k'+rR_k''+\lambda_krR_k=0,\\ X_k''-\lambda_kX_k=0,\end{array} $$
и исследуется задача Штурма — Лиувилля: при каких $$\lambda_k$$ с учетом граничных условий у этого дифференциального уравнения возможны решения. Наконец, для этих $$\lambda_k$$ решается оставшееся дифференциальное уравнение и ответ обычно записывается в виде ряда по собственным функциям оператора Штурма — Лиувилля.
Проделать эту процедуру в нашем случае не представляется возможным. Дело в том, что первое уравнение нужно решать на области $$r\in[R,\infty)$$, когда $$x\in\left[-{l/2},{l/2}\right]$$, и на области $$r\in[0,\infty)$$ в противоположном случае. Аналогично со вторым уравнением. Представить решение по всему пространству вне цилиндра в виде одного ряда по собственным функциям
Численное решение
Возвращаемся к интегральному уравнению (2) из наивного подхода. Зададимся
$$\int\limits_{-1}^{1}{dx_1\,\sigma_1(x_1)\over\sqrt{1+10000(x-x_1)^2}}+ \int\limits_{0}^{0,01}r\,dr\,\sigma_2(r)\left({1 \over\sqrt{r^2+\left(x-1\right)^2}} -{1\over\sqrt{r^2+\left(x+1\right)^2}}\right) =x.$$
Приближение к его решению можно искать не на всех функциях, а на определенном классе функций, например, на нескольких первых слагаемых разложения в степенной ряд. Отклонение получающейся функции $$\widetilde{\varphi}_a(x)$$ от правой части будем оценивать как интеграл от квадрата разности, и будем подбирать параметры функций a, добиваясь минимума этого интеграла:
$$f(a)=\int\limits_{-1}^{1}\left(\widetilde{\varphi}_a(x)-x\right)^2dx\to \text{min}.$$
Как обычно, решение попробовал найти в Maple. У меня не получилось заставить его минимизировать такой интеграл, зависящий от набора параметров. Поэтому я оставлял только один параметр, заменяя остальные их текущими значениями, строил график по этому параметру и определял его текущее значение в минимуме. Фактически выполнял вручную итерации из метода координатного спуска для функции $$f(a)$$ такого типа:
f := a -> int((
int((11.485*s + 0.584*s^3 + 0.883*s^5 + 0.587*s^7 + 0.2*s^9 + 3.57*s^11)/
sqrt(1 + 10000*(x - s)^2), s = -1 .. 1, numeric) +
int((5.01 + 5.46*10^2*r + 5.71*10^5*r^2 + 3.62*10^6*r^3 + 42.35*10^8*r^4 + a*r^5)*
r*(1/sqrt(r^2 + (1 - x)^2) - 1/sqrt(r^2 + (x + 1)^2)), r = 0 .. 0.01, numeric)
- x)^2, x = -1 .. 1, numeric)Здесь все интегралы отмечены как «numeric», чтобы Maple не пытался вычислить их аналитически. В моем случае попытка аналитического вычисления существенно замедляла работу, так что я не мог дождаться результата. Потенциал на оси для моего приближения на глаз отличается от прямой только у краев:
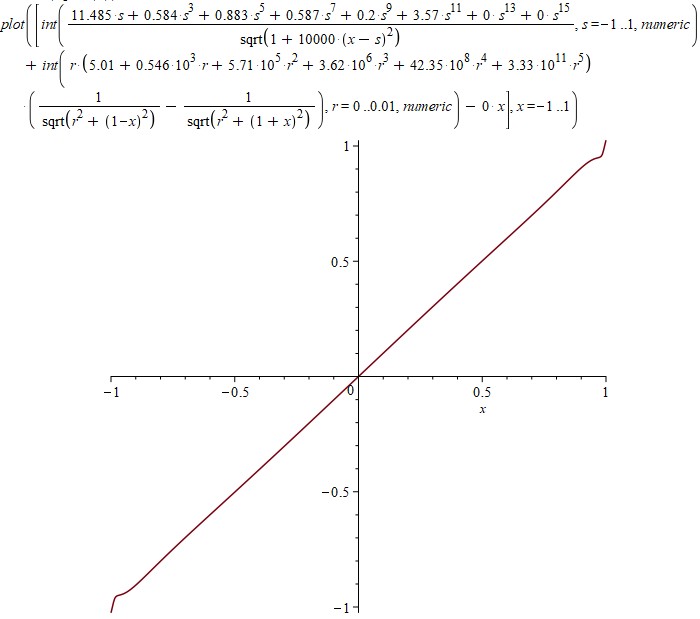
График отклонения от прямой (интеграл от квадрата этой функции я минимизировал, здесь масштаб по осям разный):
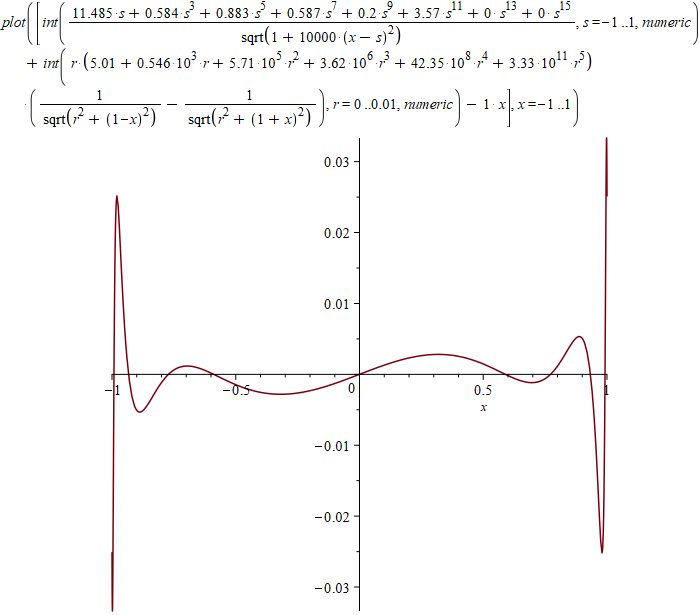
Можно также нарисовать графики плотностей на основаниях и на боковой поверхности:
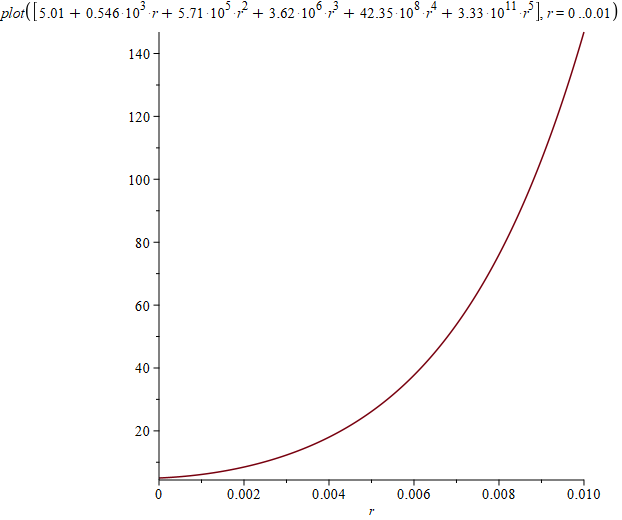
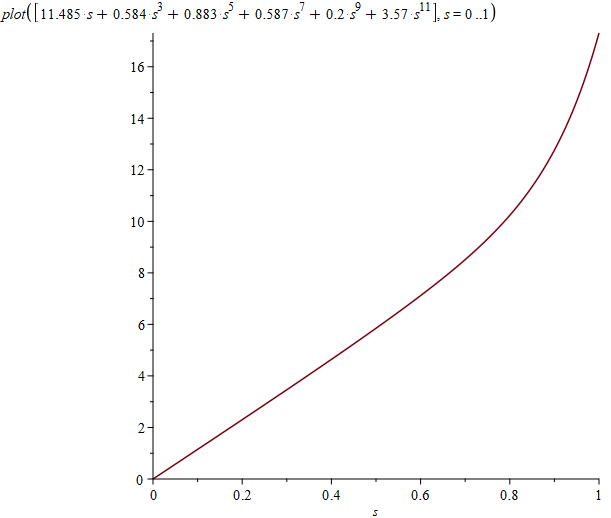
Перейдем теперь к исследованию этого решения по всему пространству. Чтобы найти потенциал в произвольной точке не на оси, нужно добавить интегрирование по углу, так как теперь расстояние от элемента поверхности до расчетной точки уже зависит от угла. Трехмерный график потенциала выглядит так:
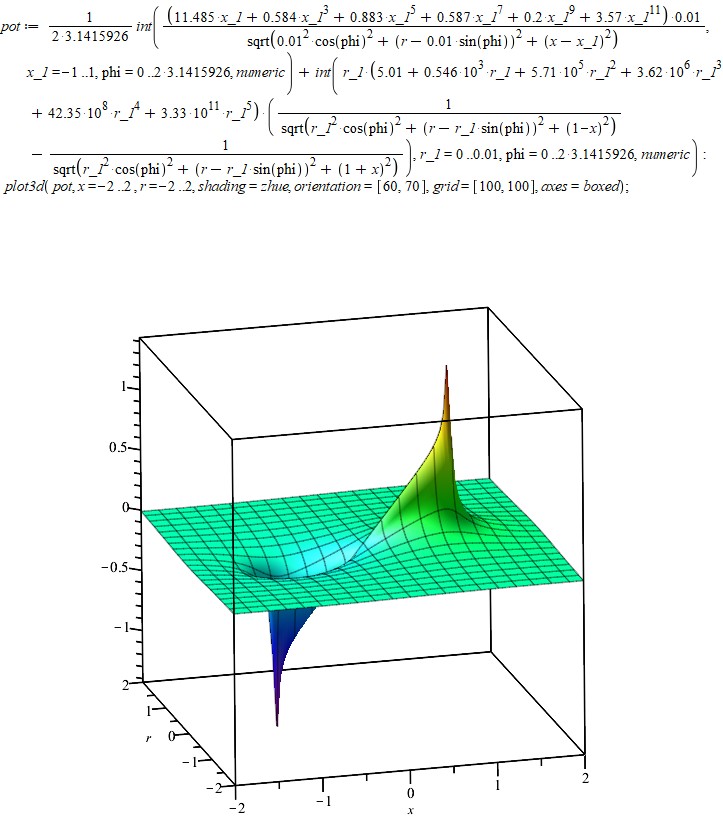
Нарисуем сечения эквипотенциальных поверхностей:
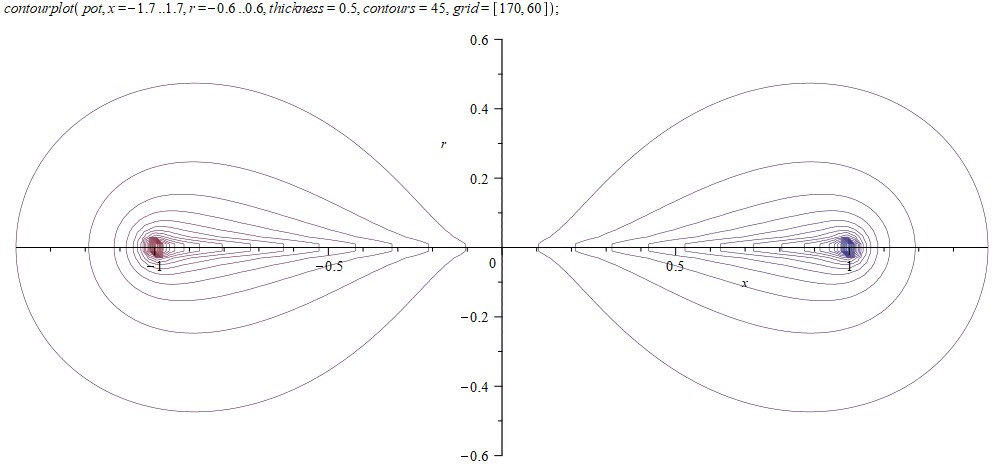
Рассмотрим поближе край проводника:
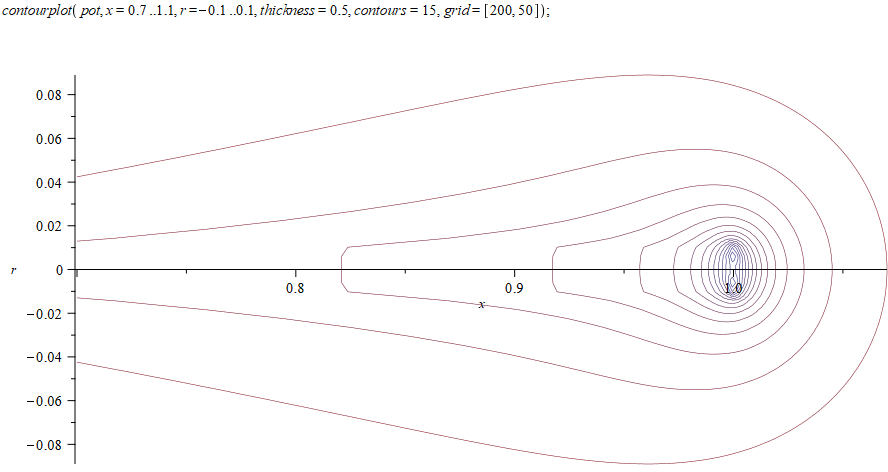
На полученный потенциал можно наложить внешнее электрическое поле и проверить, какая будет поверхность нулевого потенциала. Для правильного решения она должна совпадать с цилиндрической поверхностью проводника. В нашем случае у его краев (от 0,7 до 1) наблюдаются заметные утолщения, наглядно показывающие степень полученного приближения:
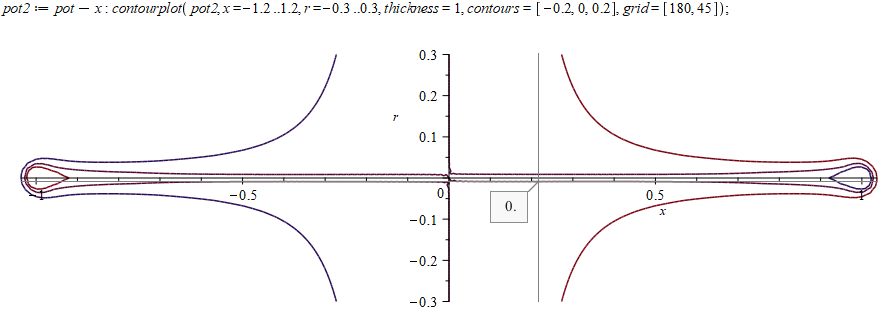
Вывод
Мы пытались решить две близких задачи: одна об электрическом поле внутри и снаружи провода с током, вторая о разделении зарядов в проводнике во внешнем электрическом поле. Аналитические методы не привели к успеху. Пришлось искать приближенное численное решение в Maple и использовать встроенные инструменты визуализации решения.
Из этого
Скрытый импульс
Недавно на гиктаймсе писали про невозможный двигатель на электромагнитной тяге. Для появления такой тяги физических оснований нет, обсуждать его мы не будем. А вот в комментариях завязалась интересная дискуссия о том, может ли замкнутая покоящаяся система изменить свой электромагнитный импульс и за счет отдачи прийти в состояние макроскопического движения. Краткий ответ — нет. Развернутый ответ — ниже.
Введение
Ранее мы рассматривали потоки электромагнитной энергии в постоянных электрических и магнитных полях. Эти потоки были замкнутыми. Однако можно составить такую систему неподвижных источников электрического и магнитного полей, в которой потоки энергии не замкнуты. Следовательно, такие системы обладают ненулевым суммарным электромагнитным импульсом.
Пример такой системы — тороидальный магнит внутри цилиндрического конденсатора. Покажем, что в ней запасается ненулевой электромагнитный импульс.
$$\begin{tikzpicture}[line width=0.21mm,scale=1.898] \coordinate (A) at (1.7,2.3); \draw[dashed,color=gray] (1.9,0.7) arc (-80:80:-0.2 and 0.8) (2.25,0.9) arc (-150:150:-0.5 and 1.2);%torus \draw[thin,dashed,color=gray] (0,1.5) ellipse (0.146 and 0.6) ++(0,-0.6) -- +(1.4,0) +(1.8,0) -- +(4,0) ++(0,1.2) -- +(1.4,0) +(1.8,0) -- +(4,0); \draw (4,1.5) ellipse (0.146 and 0.6) node {$-$} ++(0,-0.6) -- +(-0.45,0) ++(0,1.2) -- +(-0.45,0); \draw[thin,dashed,color=gray] (0,0) arc (-90:90:0.5 and 1.5);%l.ell \draw (4,0) -- (0,0) arc (270:90:0.5 and 1.5) -- +(4,0); \draw (4,1.5) ellipse (0.5 and 1.5);%r.ell \draw (-0.8,1.5) node {$+$}; \draw[thin,->] (A) -- +(0.6,0) node[right] {$\vec{S}$}; \draw[thin,->] (A) -- +(0.4,0.5) node[right] {$\vec{B}$}; \draw[thin,->] (A) -- +(0.15,-0.6) node[right] {$\vec{E}$}; \draw[opacity=0] (-0.9,0) rectangle (4.5,3); \end{tikzpicture}$$
Внутри магнита электрическое поле направлено по радиальным линиям, магнитное — по концентрическим окружностям, а вектор Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$ — вдоль оси конденсатора. Снаружи соленоида нет магнитного поля и потоков энергии. Поэтому суммарный электромагнитный импульс в такой системе направлен вдоль оси симметрии.
На первый взгляд ненулевой импульс у внешне покоящейся системы выглядит крайне странно и приводит к парадоксам. Например, при изменении тока через соленоид изменяется импульс электромагнитного поля. Система получает механический импульс отдачи и начинает перемещаться. После закачки энергии в сверхпроводящий соленоид замкнутая система без взаимодействия со внешними телами перемещается в произвольном направлении на произвольное расстояние?! Это более чем странно.
Из специальной теории относительности следует, что импульс замкнутой системы относительно центра масс равен нулю (теорема о центре масс). Следовательно, электромагнитный импульс компенсируется импульсом другой природы. Его называют «скрытым импульсом».
Впервые понятие скрытого импульса ввели Шокли и Джеймс в 1967 году. Сведения о скрытом импульсе в доступной форме систематизированы в статье «Hidden momentum, field momentum, and electromagnetic impulse» (David Babson, Stephen P. Reynolds, Robin Bjorkquist and David J. Griffiths).
Сначала докажем теорему о центре масс. Затем выведем величину скрытого импульса модельной системы, которая встречается у Шокли и Джеймса. Также объясним природу скрытого импульса в различных системах. В завершение рассмотрим основные ошибки критиков скрытого импульса.
Ниже мы употребляем понятия «импульс» и «поток энергии» как синонимы. В специальной теории относительности эти величины пропорциональны с коэффициентом $$c^2$$, так как связаны с компонентами симметричного тензора
Теорема о центре масс
Докажем, что суммарный импульс замкнутой системы относительно ее центра масс равен нулю. Мы используем тензорные обозначения четырехмерных величин.
Координаты $$X^i$$ центра масс (точнее, центра энергии):
$$X^i=\cfrac{\int x^i\,T^{00}\,d^3x}{\int T^{00}\,d^3x},$$
где плотность энергии $$T^{00}$$ определяется временной компонентой тензора
По условию теоремы координаты центра энергии не меняются со временем. Продифференцируем их по времени и приравняем к нулю:
$$\int x^i\,{\partial T^{00}\over\partial x^0}\,d^3x}=0.$$
Воспользуемся законом сохранения энергии $$\partial_\mu T^{\mu\nu}=0$$ и перепишем подынтегральное выражение:
$$x^i\,\partial_0 T^{00}=-x^i\,\partial_j T^{j0}=-\partial_j(x^iT^{j0})+T^{j0}\,\partial_j x^i=-\partial_j(x^iT^{j0})+T^{i0}.$$
Интеграл от первого слагаемого как от дивергенции приводится с помощью теоремы Гаусса к интегралу по бесконечно удаленной поверхности от нулевой (на бесконечности) функции. В итоге мы получили, что интеграл от плотности потока энергии $$T^{i0}$$ с необходимостью нулевой. Таким образом, полный поток энергии относительно центра масс системы равен 0.
Cкрытый импульс в модельной системе
Рассмотрим виток с током в однородном электрическом поле. В такой системе тоже есть ненулевой момент импульса электромагнитного поля.
Чтобы выявить природу компенсирующего скрытого импульса, применим модель витка с током постоянного сечения S, в которой носители заряда движутся свободно, без сопротивления.
$$\newcommand{\mycharge}[1][]{ \fill[red!80] (#1) circle (0.49mm); \draw[white,line width=0.21mm] (#1) +(-1pt,0) -- +(1pt,0) +(0,-1.0pt) -- +(0,1.0pt); } \begin{tikzpicture}[join=round,scale=2.109,>=stealth] \def\w{0.08} \def\p{0.1} \draw (2.5,0.5)--(2.5,1.5) [->] node[right] {$\vec{E}$}; \draw (-\p,\w)--(-\p,2-\w) [<->,gray] node[midway,left,black] {$h$}; \draw (\w,-\p)--(2-\w,-\p) [<->,gray] node[midway,below,black] {$l$}; \draw (0.25,0.25) node {$A$} (0.25,1.75) node {$B$} (1.75,0.25) node {$D$} (1.75,1.75) node {$C$}; \draw[rounded corners=1,line width=3.15mm,brown!34](\w,\w)--(2-\w,\w)--(2-\w,2-\w)--(\w,2-\w)--cycle; \foreach \x in {0.1,0.40,...,2.0} \mycharge[\x,0.08]; \foreach \x in {0.1,0.7,...,2.0} \mycharge[\x,1.92]; \foreach \x in {0.45,0.87,1.35} \mycharge[0.08,\x]; \foreach \x in {0.45,0.87,1.35} \mycharge[1.92,\x]; \draw (1.2,0.25)--(0.8,0.25) [->] node[midway,above] {$\vec{v}_1$}; \draw (1,1.75)+(-0.5,0)-- +(0.5,0) [->] node[midway,below] {$\vec{v}_2$}; \draw[opacity=0,line width=0.21mm] (-0.27,-0.30) rectangle (2.72,2); \end{tikzpicture}$$
Пусть в точке A носители заряда имеют скорость $$v_1$$. На участке AB за счет работы электрического поля их скорость растет до величины $$v_2$$. Одновременно с этим снижается плотность носителей заряда, чтобы величина тока $$I=jS=qnvS$$ оставалась постоянной: $$n_1v_1=n_2v_2$$. Далее носители движутся с постоянной скоростью до точки C, замедляются до $$v_1$$ к точке D и возвращаются на этой скорости в точку A.
В нерелятивистском случае, когда импульс одного носителя заряда есть $$p=mv$$, полный импульс носителей на участках BC и AD равен
$$P_\text{нерел}=mv_2n_2Sl-mv_1n_1Sl=0.$$
Но если учесть релятивистские эффекты, когда $$p=\gamma mv$$,
$$P_\text{рел}=\gamma_2mv_2n_2Sl-\gamma_1mv_1n_1Sl=(\gamma_2-\gamma_1){mIl\over q}.$$
Разность кинетической энергии $$K=\gamma mc^2$$ носителей на этих участках определяется работой электрического поля:
$$\gamma_2 mc^2-\gamma_1 mc^2=qEh.$$
Таким образом,
$$P_\text{скр}={IlEh\over c^2}={\mu E\over c^2},$$
где $$\mu$$ — магнитный момент витка с током.
Результат легко обобщается на случай произвольного точечного магнитного диполя в неоднородных электрических полях. Электрическое поле, перпендикулярное плоскости витка, не влияет на движение зарядов. Переходя от проекции электрического поля на плоскость витка к вектору, получаем
$$\vec{P}_\text{скр}={1\over c^2}\,\vec\mu\times\vec{E}.$$
Можно показать, что электромагнитный импульс в системе из заряда q и диполя $$\mu$$ определяется формулой
$$\vec{P}_\text{эм}=-{1\over c^2}\vec\mu\times\vec{E},$$
где $$\vec{E}=q\vec{R}/R^3$$ — электрическое поле заряда в точке, где находится диполь. Электромагнитный импульс полностью компенсируется скрытым импульсом. Мы не будем делать расчет конкретно для этой системы. Вместо этого покажем, что такая компенсация происходит всегда.
Скрытый импульс и импульс электромагнитного поля
В произвольном электростатическом поле с потенциалом $$\varphi$$ выражение для скрытого импульса витка с током I приобретает вид
$$\vec{P}_\text{скр}=-{I\over c^2}\oint\varphi\,d\vec{l}.$$
Если задана объемная плотность тока $$\vec{j}$$, то
$$\vec{P}_\text{скр}=-{1\over c^2}\int\varphi\vec{j}\,dV.$$
Подставим в последнюю формулу уравнение Максвелла для стационарных полей $$\nabla\times\vec{B}=(4\pi/c)\vec{j}$$:
$$\begin{align*} \vec{P}_\text{скр}&=-{1\over 4\pi c}\int\varphi\,\nabla\times\vec{B}\,dV=-{1\over 4\pi c}\int\left(\nabla\times\varphi\vec{B}-\nabla\varphi\times\vec{B}\right)\,dV=\\ &={1\over 4\pi c}\oint\varphi\vec{B}\times d\vec{S}-{1\over 4\pi c}\int\vec{E}\times\vec{B}\,dV=-{1\over c^2}\int\vec{S}\,dV=-\vec{P}_\text{эм}. \end{align*}$$
Первое слагаемое — интеграл по бесконечно удаленной поверхности — для замкнутых ограниченных в пространстве систем равен 0. Таким образом, мы получили, что ненулевой полный электромагнитный импульс системы всегда компенсируется скрытым импульсом. Полный импульс покоящейся стационарной системы — нулевой.
Природа скрытого импульса
Скрытый импульс связан с механическим движением носителей зарядов. Масса носителей фигурировала в выводе, но сократилась в итоговом ответе.
Скрытый импульс имеет релятивистский характер. Если бы не поправки специальной теории относительности, скрытый импульс был бы нулевым.
Природа скрытого импульса зависит от самой системы. В рассмотренной выше модели скрытый импульс (и поток энергии) связан с ускорением зарядов. В модели тока заряженной несжимаемой жидкости скрытый поток энергии вызывается перепадом давления. Во вращающемся заряженном диэлектрике (например, в сфере) импульс и поток энергии запасен в движении участков с разным механическим напряжением.
$$\begin{tikzpicture}[scale=2.109,line width=0.21mm,draw=red,node distance=4cm] \draw [fill=red!10] circle (0.7); \draw (-120:.15) [->,thin,black] arc(240:-60:.15); \def\n{12} \foreach \s in {1,...,\n} \node at ({360/\n * (\s-1)}:0.6) {$+$}; \node[fill=red!10,draw,circle] at (0,-1.3) {$+$}; \draw (0,-0.844) node {$\text{растянуто}$}; \draw (0,0.82) node {$\text{сжато}$}; \draw[line width=5,draw=black!20] (2,-0.3)+(0,-0.5) arc (270:90:0.5) -- +(2,0) node[midway,above=0.05mm] {$\text{натяжение меньше}$} arc (90:-90:0.5) -- +(-2,0) node[midway,below=-0.1mm] {$\text{натяжение больше}$}; \draw[fill=green!10,draw=green!40!black] (2,-0.3) circle(0.46) +(2,0) circle(0.46); \draw (2,-0.3) +(-120:.1) [->,thin,black] arc(240:-60:.1); \end{tikzpicture}$$
Поток механической энергии в последнем случае аналогичен потоку энергии в ременной передаче. Нижняя половина ремня на рисунке справа перемещается от нагрузки к двигателю. Она натянута больше, чем верхняя. При этом поток механической энергии направлен к нагрузке.
В настоящих электромагнитах скрытого импульса нет
В примере из введения нельзя заменить тороидальный магнит на соленоид с током. Если намотать соленоид металлическим проводом, то ни скрытого импульса внутри него, ни электромагнитного импульса снаружи не будет.
Всё дело в экранировке внешнего электрического поля в металле. Перераспределение поверхностных зарядов приводит к тому, что поверхность идеального проводника становится эквипотенциальной, и интеграл от плотности скрытого импульса $$-\varphi\vec{j}$$ зануляется.
Также исчезает и электромагнитный импульс. Электрическое поле перпендикулярно эквипотенциальным поверхностям, а вектор Пойнтинга направлен по касательным к ним. Потоки энергии текут вдоль эквипотенциальных поверхностей и вынуждены быть замкнутыми.
Ненулевое сопротивление настоящих металлов приводит к падению потенциала вдоль проводника и попаданию части потока энергии внутрь. Энергия исходит из источника тока и перемещается к проводнику, в котором переходит в тепло. Такая система уже нестационарна. В ней энергия перемещается от одной части к другой, и полный импульс отличен от нуля.
Чтобы в системе появился и электромагнитный, и скрытый импульс, вместо электромагнита надо взять неметаллический источник магнитного поля. Скрытый импульс $$-\varphi\vec{j}$$ будет запасен в молекулярных токах Ампера.
Критика скрытого импульса
Понятие скрытого импульса часто подвергается критике недостаточно компетентными авторами. Рассмотрим распространенные ошибки критиков на примере текста некоего Джеррольда Франклина.
-
В статье рассуждения начинаются не с вектора Пойнтигна, выражение для которого выводится из принципа наименьшего действия, а с применения третьего закона Ньютона к силе Лоренца. Начиная не с общих формул, а с частных, нельзя прийти к общим выводам.
-
Утверждается, что теорему о центре масс нельзя применить к электромагнитному полю, потому что взаимодействие с веществом $$-\vec{j}\cdot\vec{E}$$ нарушает равенство $$\partial_\mu T^{\mu\nu}_\text{эм}=0$$. Но правильно применять теорему к полной системе, включающей и электромагнитное поле, и вещество, а не к ее части.
-
Автор критикует модель витка с током, заявляя, что в ней появятся поверхностные заряды, компенсирующие внешнее электрическое поле. Аргумент имеет смысл только для систем с точной компенсацией зарядов разного знака вроде металлических проводников. Его легко обойти, потребовав, чтобы все заряды в витке были одного знака.
-
Еще одна грубая ошибка присутствует в предложении, по которому перераспределение зарядов по поверхности металлического проводника не приводит к исчезновению электромагнитного импульса. Суммарный ненулевой электромагнитный импульс присутствует в системе с ненулевым суммарным потоком электромагнитной энергии. Он появляется в системе с источниками и стоками энергии $$-\vec{j}\cdot\vec{E}\ne 0$$. Внутри и снаружи идеального проводника $$\vec{j}\cdot\vec{E}=0$$, электрическое поле существенно искажается и суммарный электромагнитный поток энергии исчезает.
-
Неверный логический переход в следующем выводе: во вращающихся диэлектрических заряженных телах не может быть ускорения носителей зарядов и связанной релятивистской добавки, и поэтому в ней нет скрытого импульса. На самом деле скрытый импульс есть, он имеет другую природу и связан с механическим напряжением, как мы показали выше.
Автору не удалось показать ни неприменимость теоремы о центре масс, ни отсутствие необходимости во введении понятия скрытого импульса, ни отсутствие самого скрытого импульса.
Торможение реликтовым излучением
На втором курсе за неделю перед досрочным экзаменом по теоретической физике Семен Соломонович Герштейн задал мне две задачи. В одной требовалось найти угловое распределение синхротронного излучения электрона, движущегося по окружности. Вторая оказалась интереснее: найти силу торможения со стороны реликтового излучения на площадку, движущуюся перпендикулярно самой себе. Остановимся на ней подробнее. Записей с тех времен у меня не сохранилось, а в литературе опубликованы противоречивые результаты. Хороший повод заново разобраться в задаче.
Обозначения и соглашения
Под реликтовым излучением мы подразумеваем равновесное тепловое излучение при некоторой температуре T. Напомним, что плотность энергии и давление равновесного излучения определяются температурой: ε = 4πσT4/c, P = ε/3.
В системе отсчета, связанной с реликтовым излучением, оно однородно и изотропно. Относящиеся к ней величины будем обозначать символами без штрихов. Относительно этой системы со скоростью v движется площадка (например, диск) с коэффициентом отражения R. Штрихами обозначим величины в сопутствующей системе отсчета (связанной с площадкой).
Будем опускать скорость света c в тех формулах, где она легко восстанавливается из соображений размерности.
Обзор литературы
В публикациях по этой проблеме нет консенсуса. Например, в письме Андрея Шепелева в УФН под названием «Космический микроволновой фон и аристотелевы представления о движении» приведена формула для давления на площадку $$P=-v\,(1+v^2/2)\,\varepsilon/2$$. Этот ответ, как мы увидим ниже, явно ошибочен. Автор не раскрывает вычислений, поэтому невозможно понять, где ошибка.
В работе Баласаняна и Мкртчяна «Blackbody radiation drag on a relativistically moving mirror» вычисляется плотность импульса в системе отсчета, связанной с диском, и она отождествляется с давлением (с точностью до учета отражения). По поводу этой работы у меня есть два замечания.
$$n'(\vec{k}')={1\over e^{\gamma(\omega' +k'_xv)/T}-1}.$$(1)
В то же время плотность импульса электромагнитного излучения отличается на множитель 1/c2 от вектора Поинтинга, проекции которого есть компоненты T0i тензора
$$T^{\mu\nu}=\begin{pmatrix}\varepsilon &0&0&0\\0&\varepsilon/3&0&0\\0&0&\varepsilon/3&0\\0&0&0&\varepsilon/3\end{pmatrix},$$
сразу получаем плотность импульса (см. II том Ландау и Лифшица, §35, формула 35.3)
$$S'_x=-{4\over 3}\,\varepsilon\,{v\over 1-v^2}.$$(2)
Вычисление в сопутствующей системе отсчета
$$\usetikzlibrary{decorations.pathmorphing} \begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small \tikzset{>=stealth} \tikzset{snake it/.style={->,semithick, decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate}} \def\h{3} \def\d{0.2} \def\ww{1.4} \def\w{1+\ww} \def\p{1.5} \def\r{0.7} \coordinate[label=below:$A$] (A2) at (\w,\p); \coordinate[label=above:$B$] (B2) at (\w,\p+\h); \coordinate[label=left:$C$] (C1) at (0,0); \coordinate[label=left:$D$] (D) at (0,\h); \draw[fill=blue!14](A2)--node[left]{$S$}(B2)-- ++(\d,0)-- ++(0,-\h)--cycle; \draw[gray,thin](C1)-- +(\w+\d,0); \draw[dashed,line width=0.2mm](C1)--(D); \draw[snake it](C1)--(A2) node[pos=0.5,above,inner sep=8] {$c\Delta t$}; \draw[snake it](D)--(B2); \draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$}; \draw[opacity=0](-0.40,-0.14)-- ++(0,5.06); \end{tikzpicture}$$Давление как силу на единицу поверхности определим через импульс, передаваемый диску при отражении или поглощении фотонов за единицу времени:
$$P={F\over S}={1\over S}{\hbar\Delta k\over\Delta t}.$$
Если фотоны летят под углом θ к нормали, то за время Δt до неподвижной площадки S долетят фотоны из объема S cΔt |cos θ|. Из них доля R отразится и доля (1−R) поглотится. Каждый поглощенный фотон отдаст импульс $$\hbar k\cos\theta=\hbar\omega\cos\theta/c$$, а каждый отраженный — в два раза больше. Собирая всё вместе, получаем в сопутствующей системе отсчета
$$P=\int{\hbar\omega'\cos\theta'\over S\,c\Delta t'}\,(1+R)\,S\,c\Delta t'\,|\cos\theta'|\,n'(\vec{k}')\,d^3k'.$$
Напомним, что частота ω и волновой вектор $$\vec{k}$$ образуют четырехвектор $$(\omega, \vec{k})$$. Переход к движущейся системе координат осуществляется преобразованиями Лоренца
$$\omega'={\omega-k_xv\over\sqrt{1-v^2}},\qquad k_x'={k_x-\omega v\over\sqrt{1-v^2}}.$$
Функция распределения $$n(\vec{k})$$ в фазовом пространстве инвариантна относительно преобразований Лоренца, так как и элемент фазового объема $$d^3r\,d^3k$$, и число частиц $$dN=n(\vec{r},\vec{k})\,d^3r\,d^3k$$ есть инварианты (подробнее см. II том Ландау и Лифшица, §10). Именно поэтому функция распределения в движущейся системе $$n'(\vec{k'})=n(\vec{k})$$ есть обычное распределение Бозе — Эйнштейна (1), в которое подставлена преобразованная частота.
В итоге давление определяется следующим интегралом
$$P=\int \hbar\omega'\cos\theta'\,(1+R)\,|\cos\theta'|\,{const\over exp\left(\dfrac{\hbar\omega'}{kT}\,\dfrac{1+v\cos\theta'}{\sqrt{1-v^2}}\right)-1}\,\omega'^2\,d\omega'\,{d(\cos\theta')\over 2}.$$(3)
Вместо того чтобы следить за комбинацией констант, которая в итоге должна свестись к постоянной
$$\varepsilon=\int \hbar\omega\,{const\over exp\left(\dfrac{\hbar\omega}{kT}\right)-1}\,\omega^2\,d\omega={4\pi\sigma\over c}T^4.$$
Еще отсюда видно, что (3) можно упростить, проинтегрировав по частотам. Множитель $${\sqrt{1-v^2}}/{(1+v\cos\theta')}$$ перед температурой в экспоненте появится под интегралом в четвертой степени. Дальнейшее вычисление тривиально:
$$P=\varepsilon\,(1+R)\int\limits_{-1}^{1}\cos\theta'\,|\cos\theta'|\,\dfrac{(1-v^2)^2}{(1+v\cos\theta')^4}\,{d(\cos\theta')\over 2},$$
$${\Large\boxed{P=-\varepsilon\,(1+R)\,\frac{v\,(1+v^2/3)}{1-v^2}}.}$$(4)
Чтобы убедиться в правильности результата, вычислим тем же методом давление фотонного газа на одну сторону покоящейся пластины. Зависящий от скорости подынтегральный множитель исчезает, а интеграл в пределах от 0 до 1 равен 1/3. Полное давление есть (1+R) ε/6. Если пластина всё отражает и ничего не поглощает, давление совпадает с ожидаемой величиной ε/3. Если пластина всё поглощает, давление равно ε/6 и составляет половину от давления фотонного газа ε/3. Вторая половина набегает за счет собственного излучения пластины, которое мы в наших расчетах не учитывали.
Формула (4) не совпадает ни с результатом Шепелева, который утверждает, что ответ сложен, и раскладывает его в ряд, ни с результатом Баласаняна, который ошибочно отождествляет в этой задаче плотность импульса и давление.
Вычисление в неподвижной системе отсчета
$$\usetikzlibrary{decorations.pathmorphing}
\begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small
\tikzset{>=stealth}
\tikzset{snake it/.style={->,semithick,
decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate}}
\def\h{3}
\def\d{0.2}
\def\ww{1.4}
\def\w{1+\ww}
\def\p{1.5}
\def\r{0.7}
\coordinate[label=below:$A_1$] (A1) at (\ww,\p);
\coordinate[label=above:$B_1$] (B1) at (\ww,\p+\h);
\coordinate[label=below:$A_2$] (A2) at (\w,\p);
\coordinate[label=above:$B_2$] (B2) at (\w,\p+\h);
\coordinate[label=left:$C$] (C1) at (0,0);
\coordinate[label=left:$D$] (D) at (0,\h);
\draw[fill=blue!14](A2)--(B2)-- ++(\d,0)-- ++(0,-\h)--cycle;
\draw[gray,thin](C1)-- +(\w+\d,0);
\draw[dashed,gray,fill=blue!5](A1)-- (B1)-- ++(\d,0)-- ++(0,-\h)-- cycle;
\draw[dashed,line width=0.14mm](A1)--(C1)--(D)--(B1);
\draw[snake it](C1)--(A2) node[pos=0.6,below] {$c\Delta t$};
\draw[->,semithick](\ww,\p+0.44*\h)-- +(\w-\ww,0) node[pos=0.6,above] {$v\Delta t$};
\draw[snake it](D)--(B2);
\draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$};
\draw[opacity=0](-0.40,-0.14)-- ++(0,5.06);
\end{tikzpicture}$$
Тот же результат получается и в неподвижной системе отсчета. В ней не нужно иметь дела с функцией распределения фотонов, однако
Чтобы понять, сколько летящих под углом θ фотонов с частотой ω попадет за время Δt на площадку AB, нужно ввести понятие «заметаемого объема» (объем, фотоны из которого попадут на диск) и умножить его величину на плотность фотонов nω. За это время площадка переместится из положения A1B1 в положение A2B2, а фотоны из точек C и D долетят до диска. Таким образом, заметаемый объем соответствует фигуре A1B1DС, и его величина равна S |cΔt cos θ − vΔt|.
При отражении фотона от площадки в сопутствующей системе отсчета знак проекции волнового вектора фотона изменяется на противоположный: $$k'_{2x}=-k'_{1x}$$. Найдем соответствующее изменение в неподвижной системе:
$$\begin{aligned}\Delta k &=k_{1x}-k_{2x}=k_{1x}-\gamma(k'_{2x}+\omega'_2v)=k_{1x}+\gamma(k'_{1x}-\omega'_1v)=\\&=k_{1x}+\gamma\left(\gamma(k_{1x}-\omega_1 v)-\gamma(\omega_1-k_{1x}v)v\right)=k_{1x}+\gamma^2\left(k_{1x}(1+v^2)-2v\omega\right).\end{aligned*}$$
Выражая проекцию волнового вектора через частоту фотона и азимутальный угол $$k_x=\omega\cos\theta$$, получаем
$$\Delta k=\omega\left[\cos\theta\left(1+{1+v^2\over 1-v^2}\right)-2{v\over 1-v^2}\right]={2\omega\over 1-v^2}\,(\cos\theta-v).$$
Ясно, что двойку в последнем выражении нужно заменить на (1+R), чтобы учесть случай произвольного коэффициента отражения R. Давление
$$P_\omega=\int{\hbar\omega\over S\,c\Delta t}\,{1+R\over 1-v^2}\,(\cos\theta-v)\,S|c\Delta t\cos\theta-v\Delta t|\,n_\omega\,{d(\cos\theta)\over2},$$
$$P_\omega={n_\omega\over 2}\hbar\omega\,{1+R\over 1-v^2}\int\limits_{-1}^{1}dx\,(x-v)|x-v|.$$
После вычисления интеграла и усреднения плотности энергии $$n_\omega\hbar\omega$$ по частотам получается формула (4).
Магнитные монополи, потоки энергии и квантование заряда
Мы уже рассчитывали замкнутые потоки энергии в стационарных полях зарядов и магнитов. Перейдем к более экзотическому примеру с участием не открытого на опыте магнитного монополя.
Как и в любых скрещенных электрических и магнитных полях, вокруг электрического заряда и магнитного монополя существуют потоки энергии, определяемые вектором Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$. Они замкнуты и охватывают ось симметрии системы, что может означать наличие в ней момента импульса.
Если заряд движется строго на монополь, то взаимодействие между ними отсутствует. Действительно, монополь не испытывает действие электрического поля заряда. Магнитное поле заряда на линии движения нулевое. Монополь не создает электрическое поле, а его магнитное поле коллинеарно скорости заряда, поэтому силы на заряд тоже не действуют. Отсутствие взаимодействия в этом случае наводит на мысль о том, что момент импульса остается неизменным.
По соображениям размерности момент импульса, как безразмерная величина (в единицах c = ħ = 1), не может зависеть от расстояния между зарядом и монополем — единственного размерного параметра системы. Убедимся в этом непосредственным вычислением.
Поместим электрический заряд q в точку $$\vec{a}$$ и магнитный заряд m в точку $$-\vec{a}$$. Тогда они будут создавать поля
$$\vec{E}(\vec{R})={q\over |\vec{R}-\vec{a}|^3}(\vec{R}- \vec{a}),\quad\vec{B}(\vec{R}) ={m\over |\vec{R} + \vec{a}|^3}(\vec{R} + \vec{a}).$$
Плотность импульса связана с вектором Пойнтинга
$$\vec{P} = {\vec{S} \over c^2} = {1\over 4\pi c}\vec{E}\times\vec{B}= {qm\over 4\pi c}{(\vec{R}-\vec{a})\times (\vec{R}+\vec{a})\over \left(\left(R^2+a^2\right)^2-4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$
Полный момент импульса находится интегрированием по всему пространству
$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV={qm\over 2\pi c}\int\! dV{\vec{R}\times[\vec{R}\times\vec{a}]\over \left(\left(R^2 + a^2\right)^2- 4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$
Выбираем ось z вдоль $$\vec{a}$$, угол между этой осью
$$L_z={qm\over c}\int\limits_0^{\infty}\! R^2dR\int\limits_{-1}^{1}\! d(\cos\theta){-a\,R^2\sin^2\theta\over \left(\left(R^2 + a^2\right)^2- 4(R\,a\cos\theta)^2\right)^{3/2}}.$$
Разделим числитель и знаменатель на a6 и введем новую безразмерную переменную интегрирования r = R/a. Таким образом, мы избавились от явной зависимости момента импульса от расстояний. Двойной интеграл не зависит от параметров задачи. С помощью любимого математического пакета можно убедиться, что он равен 1.
$$L_z=-{qm\over c}\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! d(\cos\theta){1-\cos^2\theta\over \left(\left(r^2 + 1\right)^2- 4r^2\cos^2\theta\right)^{3/2}}=-{qm\over c}.$$
Таким образом, момент импульса в системе заряда и монополя направлен к последнему и равен (с точностью до несущественного множителя c) произведению их величин.
В квантовой механике момент импульса квантуется. Из полуклассических соображений приравнивая полученное выше выражение для момента к минимальному значению ħ/2, мы получаем такое же ограничение на минимальные («элементарные») значения электрического и магнитного зарядов, как и в теории Дирака (где ограничение следует из дискретности прироста фазы волновой функции заряда при полном обороте вокруг монополя)
$$q_{min}\, m_{min}={\hbar c\over 2}.$$
Как видим, присутствие во Вселенной хотя бы одного монополя приводит к квантованию всех электрических зарядов.
Простейшая модель электрона: электромагнитная масса и гиромагнитное отношение
Продолжим развлекаться с классической электродинамикой. В прошлый раз мы подсчитали момент импульса в системе, состоящей из магнитного момента (маленькой катушки) в центре большой равномерно заряженной сферы
$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$(1)
Но магнитное поле вокруг сферы можно создать без дополнительной катушки, просто закрутив ее. Получается, что часть момента импульса вращающейся сферы запасается в ее электромагнитном поле. Определим эту добавку.
Магнитный момент вращающейся сферы
Мы собираемся показать, что магнитное поле вне равномерно заряженной сферы радиуса a и заряда Q, вращающейся с угловой скоростью ω, точно совпадает с полем магнитного диполя.
Начинаем с векторного потенциала
$$\vec{A}={1\over c}\int\!{\vec{j}\over r}\,dV={Q\over 4\pi ca^2}\int\!{\vec{v}\over r}\,dS={Q\over 4\pi ca^2}\int\!{\vec{\omega}\times a\vec{n}\over r}\,dS,$$
где $$r=|\vec{R}-a\vec{n}|$$ — расстояние от элемента поверхности dS, задаваемого
$$\vec{A}={Q\over 4\pi ca}\,\vec{\omega}\times\int\!{\vec{n}\over \sqrt{R^2 + a^2-2Ra\cos\chi}}\,dS={Q\over 4\pi ca}\,\vec{\omega}\times\vec{I}.$$
Интеграл $$\vec{I}$$ в последнем выражении — это усреднение единичного вектора $$\vec{n}$$ по направлениям с весом 1/r. Исходя из соображений симметрии ясно, что в результате интегрирования мы получим вектор, параллельный вектору $$\vec{R}$$. Подтвердим это вычислением.
В сферических координатах $$\inline \vec{n}=(\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)$$. Направим вектор $$\vec{R}=(0,0,R)$$ вдоль оси z. Тогда угол χ между векторами $$\inline \vec{n}$$ и $$\inline \vec{R}$$ совпадает со сферической координатой θ. Z-компонента интеграла
$$I_z=a^2\int\!\cos\theta\,{1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}\,d(\cos\theta)\,d\varphi.$$
Известно, что функцию 1/r можно разложить по многочленам Лежандра (нас интересует область R > a)
$${1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}=\sum\limits_{l=0}^\infty{a^l\over R^{l+1}}P_l(\cos\theta).$$
Подынтегральное выражение состоит из произведения этого ряда на многочлен Лежандра $$P_1(\cos\theta)=\cos\theta$$. Тогда из условия ортогональности
$$\int\limits_{-1}^{1} P_k(x)P_l(x)\,dx={2\over 2k+1}\delta_{kl}$$
сразу следует ответ
$$I_z={4\pi\over 3}{a^3\over R^2}.$$
Компоненты Ix и Iy пропорциональны интегралам от периодических функций sin φ и cos φ, и поэтому равны нулю. Переходя от проекций к вектору, для векторного потенциала получаем
$$\vec{A}={Qa^2\over 3c}\,\vec{\omega}\times{\vec{R}\over R^3}.$$
Таким образом, магнитное поле вне вращающейся сферы совпадает с полем магнитного диполя
$$\vec{\mathfrak{m}}={Qa^2\vec{\omega}\over 3c}.$$(2)
Для полноты отметим, что аналогичными вычислениями легко показать однородность магнитного поля внутри вращающейся сферы.
Электромагнитная масса
Коэффициент в (1) можно переписать
Вслед за Фейнманом мы будем называть электромагнитной массой коэффициент пропорциональности между скоростью равномерного движения сферы и импульсом электромагнитного поля. В нерелятивистском случае
$$\vec{E}=Q{\vec{R}\over R^3},\quad\vec{H}={Q\over c}{\vec{v}\times\vec{R}\over R^3}.$$
Тогда импульс электромагнитного поля дается интегралом
$$\vec{P}={1\over 4\pi c}\int\!\vec{E}\times\vec{H}\,dV={Q^2\over 4\pi c^2}\int\!{1\over R^4}\,\vec{n}\times\left[\vec{v}\times\vec{n}\right]\,dV.$$
Такой интеграл (с точностью до коэффициента) мы вычисляли в прошлый раз, поэтому сейчас просто выпишем ответ
$$\vec{P}={2Q^2 \over 3 ac^2}\,\vec{v}=m_e \vec{v}.$$
Гиромагнитное отношение и модель электрона
Теперь мы можем переписать (1) в таком виде
$$\vec{L}={m_ec\over Q}\,\vec{\mathfrak{m}}.$$
Мы получили интересный результат: гиромагнитное отношение для вращающейся безмассовой заряженной сферы совпадает с гиромагнитным отношением электрона.
Обычно в литературе по квантовой механике утверждается, что нельзя представлять себе спин электрона как его вращение, так как в такой модели скорость точек на его поверхности будет больше скорости света. Сейчас мы в этом убедимся.
Подставим в (1) магнитный момент (2) и спин электрона ½:
$${\hbar\over 2}={2\over 3}\,{Q\over ca}\,{Qa^2\omega\over 3c},$$
откуда отношение экваториальной скорости к скорости света есть
$${a\omega\over c}={9\over 4}\,{\hbar c\over Q^2}={9\over 4\alpha}\approx308.$$
Несостоятельность простейшей модели электрона проявляется и в том, что полная энергия электрического поля
$$U={1\over 8\pi}\int\!{E^2}\,dV={1\over 8\pi}\int\limits_a^{\infty}{Q^2\over R^4}\,4\pi R^2\,dR={Q^2 \over 2a}={4\over 3}\,m_ec^2$$
отличается от ожидаемой величины mec2.
Парадокс Фейнмана, или потоки энергии в постоянных электромагнитных полях
В фейнмановских лекциях по физике (выпуск 6, глава 17) есть описание следующего парадокса.
Представим, что мы конструируем прибор, в котором имеется тонкий круглый пластмассовый диск, укрепленный концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается. На диске имеется катушка из проволоки — короткий соленоид, концентричный по отношению к оси вращения. Через этот соленоид проходит постоянный ток I от маленькой батареи, также укрепленной на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одинаковым зарядом Q. Вся картина стационарна, и диск неподвижен.
Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без
какого-либо вмешательства извне. Пока через соленоид шел ток, более или менее параллельно оси диска проходил магнитный поток. После того как ток прервался, поток этот должен уменьшиться до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружностям с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внешней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вращающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнет вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую скорость.Но можно рассуждать и
по-другому. Используя закон сохранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нулевым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернется ли диск или нет? Мы предлагаем вам подумать над этим вопросом.
Решение парадокса заключается в том, что в присутствии электрических и магнитных полей имеются потоки энергии, описываемые вектором Пойнтинга $$\vec{S} \sim \vec{E} \times \vec{B}$$. В предложенной Фейнманом конфигурации эти потоки замкнуты. Поскольку поток энергии однозначно связан с плотностью импульса, наличие замкнутых потоков энергии свидетельствует о присутствии ненулевого момента импульса. Таким образом, в системе изначально был запас момента импульса, который после исчезновения магнитного поля был передан диску.
Однако есть люди, которые убеждены в том, что выражение для вектора потока энергии через векторное произведение полей годится только для переменных электромагнитных полей (действительно, перенос энергии в этом случае можно увидеть непосредственно). Им не нравится, что, согласно выражению для вектора Пойнтинга, энергия течет от источника постоянного тока к нагрузке не «по проводам», а снаружи. Основной аргумент сводится к тому, что на поток энергии легко влияют манипуляции с проводом, наличие примесей, разрывов; в то время как никакими телами снаружи, например, дополнительными зарядами или магнитами, остановить поток энергии к нагрузке не удается.
Противники применения вектора Пойнтинга в статике придумывают в этом случае другие выражения для плотности энергии, например, $$\varphi \vec{j}$$. Но такое выражение тоже не лишено недостатков, приписываемых вектору Пойнтинга. Даже если отбросить требование единообразного описания явлений и попытаться применить для зарядов и катушки выражение $$\varphi \vec{j}$$, мы сразу столкнемся с тем, что потенциал φ в точках катушки (а, значит, и и момент импульса системы) легко изменить, поместив систему внутрь большого проводящего заряженного ящика и меняя его заряд. Это плохо согласуется с гипотезой, по которой энергия, как и ток, течет по катушке.
В связи с такой критикой вектора Пойнтинга можно заняться интересным упражнением — непосредственно вычислить момент импульса электромагнитного поля через вектор Пойнтинга и сравнить его с моментом импульса, передаваемым диску. Даже если критиков эти вычисления не убедят, мы еще раз увидим красоту теории.
$$\begin{tikzpicture}[x=(-30:3cm),y=(30:3cm),z=(90:3cm),>=stealth] \def\R{1} \draw[blue,->] (0,0,0) -- (0,0,0.3\R) node[right] {$\vec{\mathfrak{m}}$}; \draw[thin] (0,0,0) -- (.7\R,.7\R,0) node[below,pos=0.5] {$a$}; \node[orange!80!black] at (0,\R,0.5*\R) {$Q$}; \def\r{0.075} \draw[blue,->,thick] (\r,0,0) arc (0:360:\r); \foreach \i in {0, 30,...,150} \draw [orange!40!black,dotted] plot [domain=-180:180, samples=30, variable=\j] (\R*cos \i*sin \j,\R*sin \i*sin \j, \R*cos \j); \foreach \j in {0, 15,...,165} \draw [orange!40!black,dotted] plot [domain=0:360, samples=60, variable=\i] (\R*cos \i*sin \j,\R*sin \i*sin \j, \R*cos \j); \end{tikzpicture}$$
Для упрощения вычислений изменим систему, предложенную Фейнманом. Будем рассматривать не заряды на краю диска, а равномерно заряженную сферу радиуса a, в центре которой находится небольшая катушка, обладающая магнитным моментом $$\vec{\mathfrak{m}}$$. Магнитный момент, находящийся в начале координат, создает в точке $$\vec{R}$$ векторный потенциал
$$\vec{A} = {\vec{\mathfrak{m}} \times \vec{R} \over R^3}$$(1)
и магнитное поле
$$\vec{H} = {3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n})-\vec{\mathfrak{m}} \over R^3}, \quad \vec{n} = {\vec{R}\over R}.$$
$$\usetikzlibrary{arrows.meta,positioning,decorations.markings,backgrounds} \colorlet{EcolFL}{orange!80!black} \tikzset{EFieldLineArrow/.style={EcolFL,decoration={markings,mark=at position 1 with {\arrow{Stealth}}},postaction={decorate}}} \def\R{0.8} \def\NE{8} \begin{tikzpicture}[-,scale=6] \foreach \i [evaluate={\angle=(\i-1)*360/\NE;}] in {1,...,\NE}{ \draw[EFieldLineArrow] (\angle:0) -- (\angle:\R); } \node[draw=EcolFL,fill=white,circle, minimum size=4cm, inner sep=0, outer sep=0] (circ) at (0,0) {}; \node[EcolFL,right] at (0.56,0.56) {$\vec{E}$} \node[blue,right] at (0.59,0.2) {$\vec{H}$} \node[right] at (0.32,0.32) {$\otimes\vec{S}$} \node[above] at (0.72,0) {$\otimes\vec{S}$} \node[right] at (0.32,-0.3) {$\otimes\vec{S}$} \node[right] at (-0.48,0.32) {$\odot\vec{S}$} \node[above] at (-0.72,0) {$\odot\vec{S}$} \node[right] at (-0.48,-0.3) {$\odot\vec{S}$} \draw [-{Latex}, blue] (0,0) -- (0,.15) node [right] {$\vec{\mathfrak{m}}$}; \begin{scope}[scale=0.3,on background layer] \foreach \a [count=\b] in {1.2}{ \draw[blue,domain=0:6.28,samples=150, line width=0.1mm, decoration={markings,% mark=at position 0.1 with {\arrowreversed{Stealth}}, mark=at position 0.4 with {\arrow{Stealth}}, mark=at position 0.5 with {\arrow{Stealth}}, mark=at position 0.6 with {\arrow{Stealth}}, mark=at position 0.9 with {\arrowreversed{Stealth}}, mark=at position 1 with {\arrowreversed{Stealth}},}, postaction=decorate] plot (xy polar cs:angle=\x r,radius={\a+\b*cos(2*\x r)}); } \end{scope} \end{tikzpicture}$$
Вектор Поинтинга есть
$$\vec{S} = {c\over 4\pi}\vec{E}\times\vec{H}.$$(2)
Он связан с плотностью импульса
$$\vec{P} = {\vec{S} \over c^2}.$$(3)
Тогда, собирая вместе, получаем
$$\vec{P} = {1\over 4\pi c}{Q \over R^2} {1 \over R^3}\left[ \vec{n}\times \left(3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n}) -\vec{\mathfrak{m}} \right) \right] = {Q\over 4\pi c R^5}\left[\vec{\mathfrak{m}} \times \vec{n}\right].$$
Момент импульса
$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV=\int\! R\,{Q\over 4\pi c R^5}\,\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]dV.$$(4)
Введем сферические координаты так, что $$\vec{\mathfrak{m}}$$ направлен вдоль оси z, а угол θ есть угол между осью z и направлением $$\vec{R}$$. Тогда
$$\vec{L}=\int\limits_a^{\infty}\!{Q\over 4\pi c R^4}R^2dR \int\!\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]d(\cos \theta)\,d\varphi.$$(5)
Первый интеграл берется элементарно. Второй есть усреднение двойного векторного произведения по всем направлениям $$\vec{n}$$, он кроме как от $$\vec{\mathfrak{m}}$$ ни от чего не зависит. Учитывая линейность интегрирования и векторного произведения, зависимость должна быть прямой пропорциональностью. Действительно, вычисления показывают, что второй интеграл равен
$$\vec{\mathfrak{m}}\int\!\sin^2\theta\,d(\cos \theta)\,d\varphi={8\pi\vec{\mathfrak{m}}\over 3}.$$
Окончательно получаем
$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$
Теперь посмотрим, какой момент импульса будет передан сфере после исчезновения магнитного поля. Начнем с момента электрических сил
$$\vec{M}=\int\!\vec{R}\times\rho\vec{E}\,dV={Q\over 4\pi}\int\!\vec{R}\times\vec{E}\,d(\cos\theta)\,d\varphi.$$
Учитывая, что вихревое электрическое поле определяется формулой
$$\vec{E}=-{1\over c}{\partial \vec{A}\over\partial t},$$
для момента импульса имеем
$$\vec{L}=\int\!\vec{M}\,dt={Q\over 4\pi c}\int\!d(\cos\theta)\,d\varphi\,\vec{R}\times\!\int\!-{\partial \vec{A}\over\partial t}dt.$$
Векторный потенциал уменьшается от начального значения $$\vec{A}$$, задаваемого формулой (1), до нуля. Поэтому последний интеграл просто равен $$\vec{A}$$. Таким образом,
$$\vec{L}=\cfrac{Q}{4\pi c a}\int\!d(\cos\theta)\,d\varphi\,\vec{n}\times \left[\vec{\mathfrak{m}} \times \vec{n}\right].$$
Это выражение совпадает с (5).
Как и ожидалось, весь момент импульса, запасенный в постоянном электромагнитном поле, передается зарядам при исчезновении магнитного поля.