Задача коллекционера
Представьте, что вы кидаете игральный кубик, и выпадает число от 1 до 6. Сколько раз в среднем нужно бросить кубик до того момента, как каждое число выпадет хотя бы один раз? Ясно, что число попыток не должно быть меньше 6. Но если при этом попадались одинаковые числа, потребуется больше бросков. Сколько именно?
Это одна из возможных формулировок задачи коллекционера. Под таким названием (Coupon Collector’s Problem) она встречается в англоязычной литературе, а в русскоязычной практически не упоминается (я нашел одну публикацию в «Математическом просвещении»). Давайте исправим несправедливость и разберем эту весьма интересную задачу.
Современному читателю проще прочувствовать смысл этой задачи на примере
Стандартное решение
Обозначим через $$T$$ искомое количество попыток сбора $$N$$ элементов коллекции. Оно состоит из суммы числа попыток $$t_i$$ получить элемент $$i$$, когда уже собрано $$i-1$$ элементов: $$T=t_1 + \cdots + t_N$$.
Вероятность найти новый $$i$$-й элемент коллекции, когда уже собрано $$i-1$$ элементов и осталось собрать $$N-i+1$$, равна
$$P(i)={N-i+1\over N}.$$(1)
То есть $$t_i$$ — случайная величина с геометрическим распределением и математическим ожиданием
$$\operatorname{E}(t_i)=\frac{1}{P(i)}=\frac{N}{N-i+1}.$$(2)
С учетом линейности математического ожидания
$$\begin{align*} \operatorname{E}(T) & {}= \operatorname{E}(t_1 + t_2 + \cdots + t_N)=\\ &=\operatorname{E}(t_1) + \operatorname{E}(t_2) + \cdots + \operatorname{E}(t_N)=\\ &=\frac{1}{P(1)} + \frac{1}{P(2)} + \cdots + \frac{1}{P(N)}=\\ &=\frac{N}{N} + \frac{N}{N-1} + \cdots + \frac{N}{1}=\\ &=N \cdot \left(\frac{1}{1} + \frac{1}{2} + \cdots + \frac{1}{N}\right)=\\ &=N H_N. \end{align*}$$
Здесь $$H_N$$ — частичные суммы гармонического ряда, асимптотика которых выражается через логарифм:
$$\operatorname{E}(T)=NH_{N}=N\ln N+\gamma N+{1\over 2}+O\left({1\over N}\right).$$(3)
Альтернативное решение
Решение выше получилось достаточно простым благодаря тому, что вероятность получения нового элемента коллекции (1) не зависит от истории, то есть от самих величин $$t_i$$. Однако такая зависимость может появиться в более сложном случае. Скажем, если коллекционер обменивается с другими коллекционерами, то чем больше у него накопилось дублей в коллекции, тем больше вероятность получить новый элемент через обмен. В этом примере формула (1) усложняется, а (2) вообще не работает.
В общем случае вероятность появления нового элемента может явно зависеть от номера шага $$t$$. Через $$P_t(n)$$ мы обозначим вероятность того, что после $$t$$ шагов мы собрали $$n$$ элементов коллекции. Я проведу рассуждения в условиях исходной задачи, а вы при необходимости можете их обобщить.
Если после выполнения $$t$$ шагов мы собрали $$n$$ элементов, это значит, что на предыдущем шаге количество элементов могло быть либо $$n-1$$, либо $$n$$. В первом случае мы получаем новый элемент с вероятностью, определяемой формулой (1), во втором случае противоположной вероятностью:
$$P_t(n)=\left(1-{n-1\over N}\right)P_{t-1}(n-1)+{n\over N}P_{t-1}(n).$$(4)
Это уравнение вместе с граничными условиями содержит в себе всю информацию из условия задачи, поэтому все остальные рассуждения будут чисто техническими.
О каких граничных условиях идет речь? Ясно, что $$P_0(0)=1$$, $$P_0(n)=0, 0<n\leq N$$ (в начале никакой коллекции нет). Кроме того, на первом шаге мы гарантированно получим один элемент, поэтому $$P_t(0)=0, t>0$$.
Перепишем для удобства (4) в другом виде после подстановки $$n=N-m$$:
$$P_t(N-m)={m+1\over N}P_{t-1}\left(N-(m+1)\right)+{N-m\over N}P_{t-1}(N-m)$$(4a)
Заметим еще, что на каждом шаге должна сохраняться нормировка вероятности — в коллекции точно должно быть хоть
$$\sum_{n=0}^N P_t(n)=1.$$(5)
Нарушение условия нормировки сразу укажет на ошибку в построении математической модели. Давайте проверим, что в (4) подобных ошибок нет:
$$\begin{align*} \sum_{n=0}^N P_t(n)&=P_t(0)+\sum_{n=1}^N \left[\left(1-{n-1\over N}\right)P_{t-1}(n-1)+{n\over N}P_{t-1}(n)\right]=\\ &=\sum_{n=0}^{N-1} \left(1-{n\over N}\right)P_{t-1}(n)+\sum_{n=1}^N {n\over N}P_{t-1}(n)=\\ &=\sum_{n=0}^{N-1}P_{t-1}(n)-{0\over N}P_{t-1}(0)+{N\over N}P_{t-1}(N)=\\ &=\sum_{n=0}^{N}P_{t-1}(n). \end{align*}$$
Мы опустили нулевое слагаемое $$P_t(0)$$ из граничных условий, а также перенумеровали слагаемые в одной из сумм. По индукции видно, что нормировка сохраняется на каждом шаге.
В задаче нам нужно усреднить число попыток $$t$$ до окончания сбора коллекции:
$$\operatorname{E}(T)=\sum\limits_tt\left(P_t(N)-P_{t-1}(N)\right).$$
Чтобы получить вероятность окончания сбора коллекции именно на шаге $$t$$, я вычел из вероятности собрать $$N$$ элементов на шаге $$t$$ вероятность собрать $$N$$ элементов на шаге $$t-1$$ (вычитается вероятность того, что на предыдущем шаге коллекция уже собрана).
Из (4а) при $$m=0$$:
$$P_t(N)={1\over N}P_{t-1}\left(N-1\right)+P_{t-1}(N).$$
Отсюда
$$\operatorname{E}(T)={1\over N}\sum\limits_ttP_{t-1}(N-1).$$(6)
Здесь мы видим другое представление вероятности окончания сбора коллекции: вероятность сбора последнего элемента $$1/N$$ умножается на вероятность наличия $$N-1$$ элементов на предыдущем шаге.
Идея дальнейших вычислений в том, чтобы пользуясь равенством (4а) и дальше понижать аргумент в (6) от $$N-1$$ до 0. Тогда в сумме останется только один ненулевой элемент, соответствующий $$P_0(0)=1$$. Вы можете проделать несколько подстановок (4а) вручную и увидеть закономерность. Я же сразу сформулирую ее в виде утверждения, связывающего $$\operatorname{E}(T)$$ и $$P_{t}(N-m)$$:
Утверждение. Существуют такие числа $$A_m$$ и $$B_m$$, что при любых натуральных $$N$$ и $$m\in [1,N]$$ выполняется равенство
$$\operatorname{E}(T)={m\over N}\sum\limits_ttP_{t-m}(N-m)+A_mN-B_m.$$(7)
Доказательство по индукции. Если $$m=1$$, то из (6) гипотеза верна при $$A_1=B_1=0$$. Пусть она верна для $$m>1$$. Тогда из (4а)
$$\begin{align*}\operatorname{E}(T)&={m\over N}\sum_tt\left[{m+1\over N}P_{t-m-1}\left(N-(m+1)\right)+{N-m\over N}P_{t-m-1}(N-m)\right]+A_mN-B_m=\\ &={m\over N}{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+{N-m\over N}\underbrace{{m\over N}\sum_ttP_{t-m-1}(N-m)}_{S_1}+A_mN-B_m.\end{align*}$$
Сумма в первом слагаемом похожа на нужную сумму из (7) для $$m$$, увеличенного на 1. Пока отдельно вычислим оставшуюся сумму:
$$\begin{align*}S_1&={m\over N}\sum\limits_ttP_{t-m-1}(N-m)=\\ &={m\over N}\sum_{t+1}(t+1)P_{t-m}(N-m)=\\ &={m\over N}\sum_ttP_{t-m}(N-m)+{m\over N}\sum_tP_{t-m}(N-m)=\\ &=\operatorname{E}(T)-A_mN+B_m+\underbrace{{m\over N}\sum_tP_t(N-m)}_{S_2}.\end{align*}$$
Здесь мы дважды воспользовались изменением индекса суммирования. Так как суммирование идет по всем возможным $$t$$, мы можем спокойно менять индексы. Лишних или отсутствующих слагаемых не будет, так как вероятности зануляются, когда число шагов меньше размера коллекции: $$P_t(n)=0, t<n$$.
Просуммируем теперь (4a) по всем $$t$$:
$$\begin{align*}\sum_tP_t(N-m)&=\sum_t{m+1\over N}P_{t-1}\left(N-(m+1)\right)+\sum_t{N-m\over N}P_{t-1}(N-m)=\\ &={m+1\over N}\sum_tP_t\left(N-(m+1)\right)+{N-m\over N}\sum_tP_t(N-m), \end{align*}$$
откуда
$${m\over N}\sum_tP_t(N-m)=\sum_t{m+1\over N}P_t\left(N-(m+1)\right).$$
Таким образом, по индукции $$\inlineS_2={m\over N}\sum_tP_t(N-m)$$ не зависит от $$m$$ и равно 1, так как при $$m=N$$ переходит в $$P_0(0)+P_1(0)+P_2(0)+\ldots=1+0+0+\ldots=1$$. Возвращаемся к $$\operatorname{E}(T)$$:
$$\begin{align*}\operatorname{E}(T)&={m\over N}{m+1\over N}\sum\limits_ttP_{t-m-1}\left(N-(m+1)\right)+\\ &+{N-m\over N}(\operatorname{E}(T)-A_mN+B_m+1)+A_mN-B_m,\\ N\operatorname{E}(T)&=m{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+\\&+\operatorname{E}(T)N-A_mN^2+B_mN+N-m\operatorname{E}(T)+mA_mN-mB_m-m+A_mN^2-B_mN,\\ m\operatorname{E}(T)&=m{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+N+mA_mN-mB_m-m,\\ \operatorname{E}(T)&={m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+(A_m+{1/m})N-(B_m+1).\end{align*}$$
По форме это совпадает с (7) при условии
$$A_{m+1}=A_m+{1\over m},\quad B_{m+1}=B_m+1.$$
С учетом начальных условий $$A_1=B_1=0$$ получаем явные выражения коэффициентов: $$A_m=1+1/2+\ldots+1/(m-1)=H_{m-1}$$ — частичные суммы гармонического ряда, $$B_m=m-1$$. $$\square$$
Подставим теперь $$m=N$$ в (7). Тогда
$$\omeratorname{E}(T)=\sum_ttP_{t-N}(0)+H_{N-1}N-N+1=H_{N-1}N+1=N\left(H_{N-1}+{1\over N}\right)=NH_N,$$
что совпадает с ответом стандартного решения.
Вывод
Мы решили задачу коллекционера, записав уравнение эволюции распределения вероятности (4). Это уравнение можно рассматривать как дискретный вариант уравнения, описывающего поток вероятности.
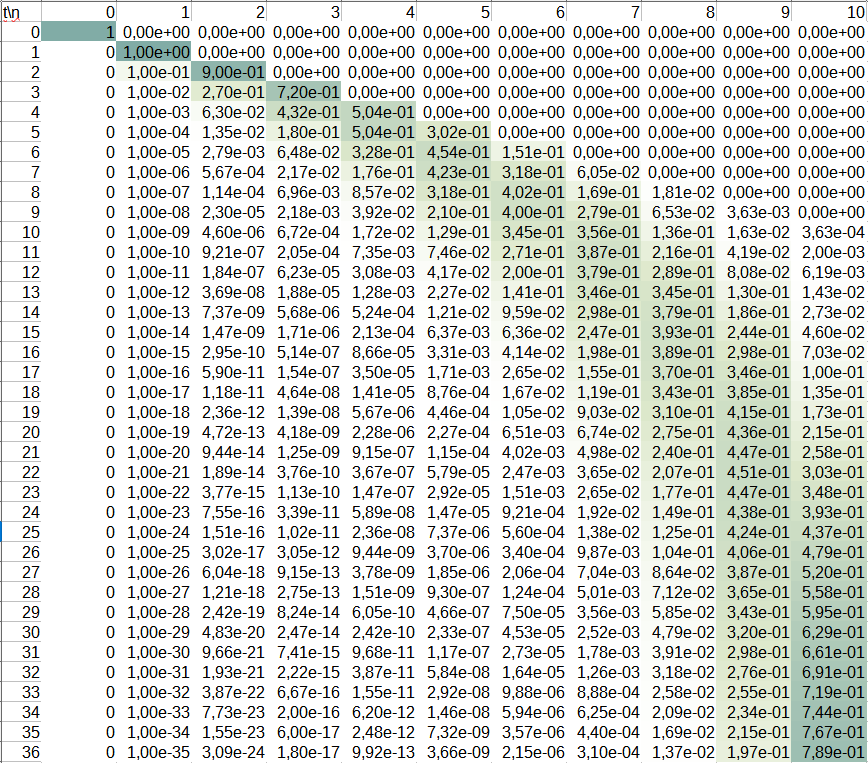
Такой подход универсален для задач подобного типа, потому что позволяет их решать не только аналитически, но и численно. Например, в нашем случае эволюцию распределения вероятности можно рассчитать на основе уравнения (4) даже в Excel. На скриншоте видно, как распределение вероятности со временем смещается от меньших $$n$$ к большим для $$N=10$$.
Оставьте свой комментарий