Хоккейная задача — 2
Продолжим решать «хоккейную задачу». В прошлом посте мы рассмотрели вариант задачи с искусственной поддержкой постоянной скорости вращения кольца. Перейдем теперь к варианту, когда за счет трения замедляется не только поступательное движение, но и вращение.
Напомним, что динамика кольца описывается уравнениями
$$\begin{align*} {du\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{u-v\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}},\\ {dv\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{v-u\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}}, \end{align*}$$(1)
где $$v$$ — скорость поступательного движения, $$u=\omega R$$ — скорость вращательного движения кольца.
Система уравнений (1) симметрична относительно замены $$u$$ на $$v$$. Если в начальный момент $$u=v$$, то по соображениям симметрии это соотношение будет сохраняться между скоростями вплоть до остановки. Другой случай, который мы рассмотрим — это $$u>v$$. Противоположный случай $$u<v$$ будет вытекать из него простой заменой $$u$$ на $$v$$ из тех же соображений симметрии.
Вырожденный случай u = v
Оба уравнения системы принимают один и тот же вид
$${dv\over dt}=-\int\limits_0^{2\pi}{d\alpha\over 2\pi\sqrt2}\,\sqrt{1-\sin\alpha}={2\over\pi}.$$
Скорости совместного движения падают линейно со временем, но в $$\pi/2=1,\!57$$ раз медленнее отдельного вращения или отдельного поступательного движения.
Случай u > v
К сожалению, интегралы в системе (1) сводятся к эллиптическим, что не оставляет надежды решить систему аналитически. Остается численное решение.
Прямая попытка решить уравнение в Maple проваливается. Определенные интегралы заменяются нагромождением эллиптических интегралов, приводить которое здесь нет смысла. При построении графика мы видим сообщение об ошибке
Warning, cannot evaluate the solution past the initial point, problem may be complex, initially singular or improperly set up
Чтобы упростить выражения, накладываем ограничение $$u(t)\ge v(t)\ge 0$$ на каждый из интегралов.
sys_ode := {
diff(u(t), t) = -`assuming`(
[int(
(u(t)-v(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
)/(2*Pi),
diff(v(t), t) = -`assuming`(
[int(
(v(t)-u(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
)/(2*Pi), u(0) = 10, v(0) = 1
};Ограничения устраняют сообщение об ошибке. Maple надолго задумывается, но выводит пустой график. Чтобы понять причину, выведем решение уравнения в
p := dsolve(sys_ode, type = numeric):
p(1);$$[t=1.,\\u(t)=10.9976102709142-2.84005015829721 10^{-8}{\rm I},\\v(t)=1.04887416587408+2.92542849266058 10^{-8}{\rm I}]$$
Накопление ошибки округления приводит к появлению ненулевой мнимой части в искомых функциях,
sys_ode := {
diff(u(t), t) = -Re(`assuming`(
[int(
(u(t)-v(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
))/(2*Pi),
diff(v(t), t) = -Re(`assuming`(
[Re(int(
(v(t)-u(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
))/(2*Pi), u(0) = 10, v(0) = 1
};Наконец, Maple, долго думая, всё же рисует график.
plots[odeplot](p, [
[t, (10-t), color=gray],
[t, sqrt(1-(1/10)*t), color=gray],
[t, u(t), color = blue],
[t, v(t), color = red]
], 0 .. 11);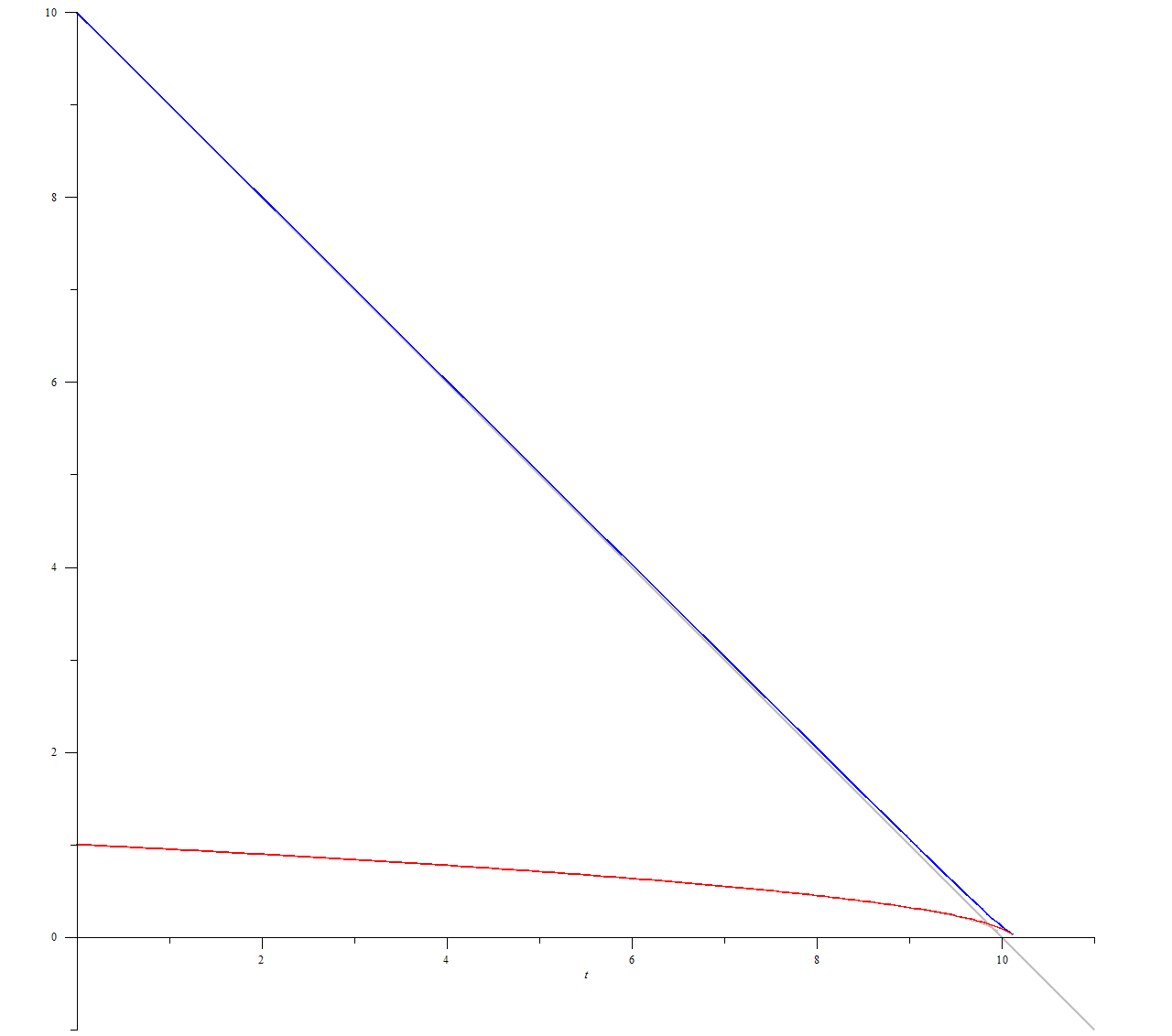
При этом мы видим предупреждение о точке остановки вычислений, которая, очевидно, совпадает с моментом окончания движения:
Warning, cannot evaluate the solution further right of 10.155665, probably a singularity
Для численного решения мы выбрали начальную поступательную скорость 1 и скорость вращения 10. Без вращения кольцо перемещается в течение 1 единицы времени на расстояние 0,5. Наличие вращения привело к тому, что поступательное движение сохранялось более 10 единиц времени.
Линеаризованное решение при u >> v
График $$u(t)$$ — синяя линия — практически совпадает с прямой. График $$v(t)$$ — красная линия — напоминает параболу. Такое поведение предсказывается линеаризованным решением в пределе $$u\gg v$$. Пренебрегая $$v$$ в первом уравнении системы (1) и раскладывая второе по степеням $$p=v/u$$, получаем
$$\begin{align*} {du\over dt}&=-1,\\ {dv\over dt}&=-{v\over 2u}. \end{align*}$$(2)
Решением этой системы являются функции $$u(t)=u_0-t$$, $$v(t)=v_0\sqrt{1-t/u_0}$$. Их графики изображены серыми линиями.
Как видим из численного решения и графика, приближение верно описывает характер движения, пока $$u$$ и $$v$$ не становятся сравнимыми. Вот график для случая, когда одна скорость в два раза больше другой:
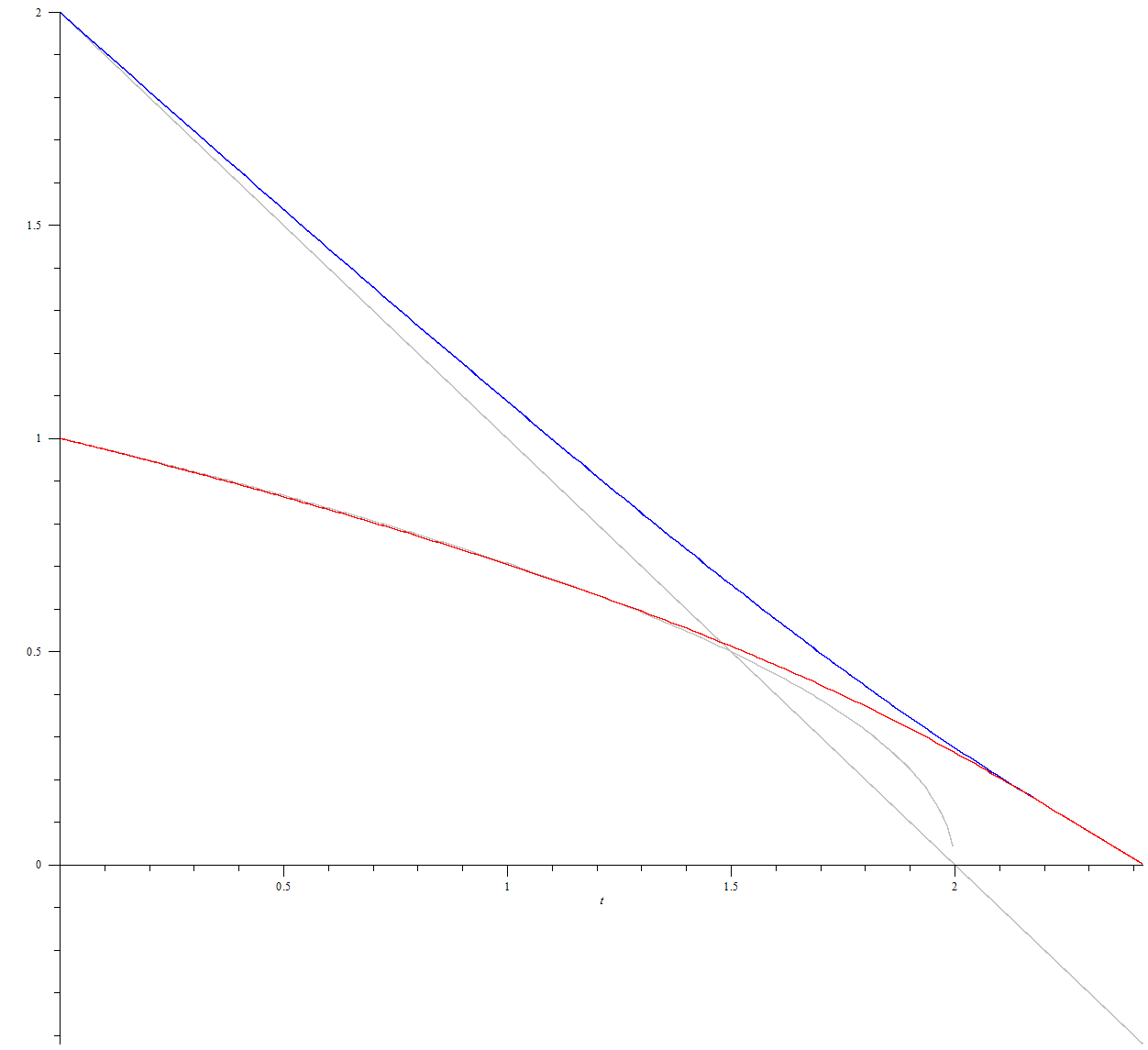
Здесь отличие от линеаризованного решения заметно практически сразу.
Путь до остановки: линеаризованное приближение
Пройденный кольцом путь дается площадью криволинейной трапеции под красной линией. В линеаризованном приближении криволинейная трапеция ограничена параболой и, как легко видеть, имеет площадь $$l=2u_0v_0/3$$. Если бы кольцо не вращалось, оно прошло бы расстояние $$l_0=v_0^2/2$$. Таким образом, чтобы увеличить проходимый путь в 5 раз, нужно закрутить кольцо с угловой скоростью
$$\omega_0={u_0\over R}={15\over 4}{v_0\over R}.$$
Напомним, что для прохождения кольцом того же пути при постоянном поддержании вращения его скорость должна быть в три раза меньше: $$\omega_0=(5/4)\,{v_0/R}$$.
Путь до остановки: численное решение
Теперь вычислим проходимый путь из первоначальных уравнений, без линеаризации.
Maple
dsol2p := dsolve(sys_ode, type = numeric, output = listprocedure):
v := eval(v(t), dsol2p):
v(4.04);$$0.00664275658541608$$
v(4.05);$$0.000276558860981139$$
v(4.06);$$0.00946581059191108$$
int(v(t), t = 0 .. 4.05);$$2.5535588257745343$$
Последний результат Maple вычислял больше 10 минут. Как видим, для начального значения 15/4 погрешность линеаризованного приближения составляет 2%.
Вывод
Мы решили «хоккейную задачу» в исходной упрощенной формулировке и без упрощений в линеаризованном приближении. С помощью системы компьютерной алгебры Maple убедились, что для условия этой задачи линеаризованное приближение дает ошибку на несколько процентов.
Хоккейная задача
В 2007 году на физтеховской олимпиаде по физике была такая задача:
Тонкое кольцо лежит на шероховатой горизонтальной поверхности. После толчка в направлении центра кольца оно перемещается на некоторое расстояние. Когда это кольцо раскрутили до некоторой угловой скорости (поддерживаемой постоянной за всё время движения), то при той же начальной скорости кольцо прошло в $$k$$ раз большее расстояние. Как было раскручено это кольцо? (попытайтесь в ответе найти нелинейную поправку). (В.С. Булыгин)
На примере этой задачи я хочу показать, как использовать системы компьютерной алгебры, в частности, Maple.
В условии поддержка постоянной угловой скорости вращения выглядит искусственно. Это требование упрощает задачу, чтобы ее можно было решить на олимпиаде. В этом посте рассмотрим такую формулировку, а в следующем — потерю через трение не только поступательной скорости, но и вращательной.
Физическая сторона задачи
Решение задачи разобрано на Элементах (там ее назвали «хоккейной задачей»). Физическая часть решения не требует выхода за рамки школьных знаний, на ней останавливаться не будем. А вот на математике остановимся подробнее. Начнем с системы уравнений, выведенной по ссылке выше:
$$\begin{align*} {du\over dt}&=-\mu g\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{u-v\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}},\\ {dv\over dt}&=-\mu g\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{v-u\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}}. \end{align*}$$(1)
Здесь $$v$$ — скорость поступательного движения, $$u=\omega R$$ — скорость вращательного движения кольца.
Уравнения таковы, что соответствующим выбором единицы измерения времени мы можем избавиться от несущественного множителя $$\mu g$$, поэтому в рассуждениях ниже мы его опустим.
Предельный режим
В предположении $$u=const$$ уравнение на $$v$$ имеет простой предельный режим, когда $$v\to 0$$. Тогда раскладывая подынтегральное выражение в ряд по $$v$$ с точностью до второго порядка малости и интегрируя, видим, что убывание скорости пропорционально самой скорости. При малых скоростях кольцо останавливается по экспоненте, как будто трение не сухое, а жидкостное.
Случай постоянной скорости вращения
По условию угловая скорость вращения поддерживается постоянной, а линейная скорость падает до 0. Логично предположить, что мы имеем дело с режимом $$0<v<u=\text{const}$$. Пусть $$p=v/u$$. Тогда
$$u{dp\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{p-\sin\alpha\over\sqrt{1+p^2-2p\sin\alpha}}.$$(2)
До остановки кольцо проходит расстояние
$$l=\int\limits_0^{t_\text{ост}} v\,dt=u\int\limits_0^{t_\text{ост}} p\,dt.$$(3)
Подставим $$dt$$ из (2) в (3):
$$u^2\int\limits_{p_0}^0{p\,dp\over-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{p-\sin\alpha\over\sqrt{1+p^2-2p\sin\alpha}}}=u\int\limits_0^{t_\text{ост}} p\,dt=l.$$(4)
Когда вращения нет, кольцо движется равнозамедленно и проходит расстояние $$l_0=v_0^2/2$$. Вращающееся кольцо проходит в $$k=5$$ раз большее расстояние $$l$$:
$$l=kl_0=k\,{v_0^2\over 2}=ku^2\,{p_0^2\over 2}.$$
Подставим $$l$$ в (4) и поделим на $$p_0^2$$:
$${1\over p_0^2}\int\limits^{p_0}_0{p\,dp\over\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{p-\sin\alpha\over\sqrt{1+p^2-2p\sin\alpha}}}={k\over 2}.$$(5)
Это уравнение дает нам соотношение между начальной скоростью вращения кольца $$\omega_0=v_0/(p_0R)$$ и ростом проходимого до остановки расстояния $$k$$.
Численное решение в Maple
Внутренний интеграл выражается через эллиптические интегралы. Однако Maple ничего не знает про знак $$p$$ и выдает слишком громоздкое выражение, содержащее фрагменты вроде $$\sqrt{-{2p/(p-1)^2}}$$, csgn(p-1). Подскажем очевидное ограничение на $$p$$:
`assuming`([
int(
(p-sin(alpha))/(2*Pi*sqrt(p^2 + 1 - 2*p*sin(alpha))),
alpha = 0 .. 2*Pi
)
], [p > 0]):
factor(%);
$${\left(p-1\right)\mathrm{EllipticK}\left(\dfrac{2\sqrt{p}}{p+1}\right)+\left(p+1\right)\mathrm{EllipticE}\left(\dfrac{2\sqrt{p}}{p+1}\right)\over p\pi}$$
После этого легко подобрать ответ $$p_0$$ с нужной точностью:
p0 := 0.78:
(int(
p^2 * Pi / (
(p-1) * EllipticK(2*sqrt(p)/(p+1)) +
(p+1) * EllipticE(2*sqrt(p)/(p+1))
),
p = 0 .. p0
)) / p0^2;
$$2.491446599$$
В начальный момент скорости поступательного движения и вращения были связаны соотношением $$v_0\approx0,\!78\,\omega_0R$$.
Приближенный ответ можно получить не только численно, но и из разложения внутреннего интеграла в ряд
expand(series(`assuming`([int(...)], [p >= 0]), p = 0, 8));
$${1\over 2}p+{1\over 16}p^3+{3\over 128}p^5+O(p^7)$$
Вычислим левую часть (5) при $$p_0=0,\!78$$, последовательно уточняя разложение внутреннего интеграла:
$$\begin{align*} &{1\over 0,\!78^2}\int\limits_0^{0,78}{p\over{\frac{1}{2}p}}\,dp=2,\!564102564,\\ &{1\over 0,\!78^2}\int\limits_0^{0,78}{p\over{\frac{1}{2}p+{1\over 16}p^3}}\,dp=2,\!501916372,\\ &{1\over 0,\!78^2}\int\limits_0^{0,78}{p\over{\frac{1}{2}p+{1\over 16}p^3+{3\over 128}p^5}}\,dp=2,\!493976851. \end{align*}$$
Хотя начальное значение параметра $$p_0=v_0/u_0=0,\!78$$ нельзя назвать малым, линеаризация по этому параметру дает погрешность менее 3%. Для линейного приближения ответ составил бы $$p_0=4/k=0,\!8\,$$. А учет кубической поправки уже дает погрешность меньше процента.
Скрытый импульс
Недавно на гиктаймсе писали про невозможный двигатель на электромагнитной тяге. Для появления такой тяги физических оснований нет, обсуждать его мы не будем. А вот в комментариях завязалась интересная дискуссия о том, может ли замкнутая покоящаяся система изменить свой электромагнитный импульс и за счет отдачи прийти в состояние макроскопического движения. Краткий ответ — нет. Развернутый ответ — ниже.
Введение
Ранее мы рассматривали потоки электромагнитной энергии в постоянных электрических и магнитных полях. Эти потоки были замкнутыми. Однако можно составить такую систему неподвижных источников электрического и магнитного полей, в которой потоки энергии не замкнуты. Следовательно, такие системы обладают ненулевым суммарным электромагнитным импульсом.
Пример такой системы — тороидальный магнит внутри цилиндрического конденсатора. Покажем, что в ней запасается ненулевой электромагнитный импульс.
$$\begin{tikzpicture}[line width=0.21mm,scale=1.898] \coordinate (A) at (1.7,2.3); \draw[dashed,color=gray] (1.9,0.7) arc (-80:80:-0.2 and 0.8) (2.25,0.9) arc (-150:150:-0.5 and 1.2);%torus \draw[thin,dashed,color=gray] (0,1.5) ellipse (0.146 and 0.6) ++(0,-0.6) -- +(1.4,0) +(1.8,0) -- +(4,0) ++(0,1.2) -- +(1.4,0) +(1.8,0) -- +(4,0); \draw (4,1.5) ellipse (0.146 and 0.6) node {$-$} ++(0,-0.6) -- +(-0.45,0) ++(0,1.2) -- +(-0.45,0); \draw[thin,dashed,color=gray] (0,0) arc (-90:90:0.5 and 1.5);%l.ell \draw (4,0) -- (0,0) arc (270:90:0.5 and 1.5) -- +(4,0); \draw (4,1.5) ellipse (0.5 and 1.5);%r.ell \draw (-0.8,1.5) node {$+$}; \draw[thin,->] (A) -- +(0.6,0) node[right] {$\vec{S}$}; \draw[thin,->] (A) -- +(0.4,0.5) node[right] {$\vec{B}$}; \draw[thin,->] (A) -- +(0.15,-0.6) node[right] {$\vec{E}$}; \draw[opacity=0] (-0.9,0) rectangle (4.5,3); \end{tikzpicture}$$
Внутри магнита электрическое поле направлено по радиальным линиям, магнитное — по концентрическим окружностям, а вектор Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$ — вдоль оси конденсатора. Снаружи соленоида нет магнитного поля и потоков энергии. Поэтому суммарный электромагнитный импульс в такой системе направлен вдоль оси симметрии.
На первый взгляд ненулевой импульс у внешне покоящейся системы выглядит крайне странно и приводит к парадоксам. Например, при изменении тока через соленоид изменяется импульс электромагнитного поля. Система получает механический импульс отдачи и начинает перемещаться. После закачки энергии в сверхпроводящий соленоид замкнутая система без взаимодействия со внешними телами перемещается в произвольном направлении на произвольное расстояние?! Это более чем странно.
Из специальной теории относительности следует, что импульс замкнутой системы относительно центра масс равен нулю (теорема о центре масс). Следовательно, электромагнитный импульс компенсируется импульсом другой природы. Его называют «скрытым импульсом».
Впервые понятие скрытого импульса ввели Шокли и Джеймс в 1967 году. Сведения о скрытом импульсе в доступной форме систематизированы в статье «Hidden momentum, field momentum, and electromagnetic impulse» (David Babson, Stephen P. Reynolds, Robin Bjorkquist and David J. Griffiths).
Сначала докажем теорему о центре масс. Затем выведем величину скрытого импульса модельной системы, которая встречается у Шокли и Джеймса. Также объясним природу скрытого импульса в различных системах. В завершение рассмотрим основные ошибки критиков скрытого импульса.
Ниже мы употребляем понятия «импульс» и «поток энергии» как синонимы. В специальной теории относительности эти величины пропорциональны с коэффициентом $$c^2$$, так как связаны с компонентами симметричного тензора
Теорема о центре масс
Докажем, что суммарный импульс замкнутой системы относительно ее центра масс равен нулю. Мы используем тензорные обозначения четырехмерных величин.
Координаты $$X^i$$ центра масс (точнее, центра энергии):
$$X^i=\cfrac{\int x^i\,T^{00}\,d^3x}{\int T^{00}\,d^3x},$$
где плотность энергии $$T^{00}$$ определяется временной компонентой тензора
По условию теоремы координаты центра энергии не меняются со временем. Продифференцируем их по времени и приравняем к нулю:
$$\int x^i\,{\partial T^{00}\over\partial x^0}\,d^3x}=0.$$
Воспользуемся законом сохранения энергии $$\partial_\mu T^{\mu\nu}=0$$ и перепишем подынтегральное выражение:
$$x^i\,\partial_0 T^{00}=-x^i\,\partial_j T^{j0}=-\partial_j(x^iT^{j0})+T^{j0}\,\partial_j x^i=-\partial_j(x^iT^{j0})+T^{i0}.$$
Интеграл от первого слагаемого как от дивергенции приводится с помощью теоремы Гаусса к интегралу по бесконечно удаленной поверхности от нулевой (на бесконечности) функции. В итоге мы получили, что интеграл от плотности потока энергии $$T^{i0}$$ с необходимостью нулевой. Таким образом, полный поток энергии относительно центра масс системы равен 0.
Cкрытый импульс в модельной системе
Рассмотрим виток с током в однородном электрическом поле. В такой системе тоже есть ненулевой момент импульса электромагнитного поля.
Чтобы выявить природу компенсирующего скрытого импульса, применим модель витка с током постоянного сечения S, в которой носители заряда движутся свободно, без сопротивления.
$$\newcommand{\mycharge}[1][]{ \fill[red!80] (#1) circle (0.49mm); \draw[white,line width=0.21mm] (#1) +(-1pt,0) -- +(1pt,0) +(0,-1.0pt) -- +(0,1.0pt); } \begin{tikzpicture}[join=round,scale=2.109,>=stealth] \def\w{0.08} \def\p{0.1} \draw (2.5,0.5)--(2.5,1.5) [->] node[right] {$\vec{E}$}; \draw (-\p,\w)--(-\p,2-\w) [<->,gray] node[midway,left,black] {$h$}; \draw (\w,-\p)--(2-\w,-\p) [<->,gray] node[midway,below,black] {$l$}; \draw (0.25,0.25) node {$A$} (0.25,1.75) node {$B$} (1.75,0.25) node {$D$} (1.75,1.75) node {$C$}; \draw[rounded corners=1,line width=3.15mm,brown!34](\w,\w)--(2-\w,\w)--(2-\w,2-\w)--(\w,2-\w)--cycle; \foreach \x in {0.1,0.40,...,2.0} \mycharge[\x,0.08]; \foreach \x in {0.1,0.7,...,2.0} \mycharge[\x,1.92]; \foreach \x in {0.45,0.87,1.35} \mycharge[0.08,\x]; \foreach \x in {0.45,0.87,1.35} \mycharge[1.92,\x]; \draw (1.2,0.25)--(0.8,0.25) [->] node[midway,above] {$\vec{v}_1$}; \draw (1,1.75)+(-0.5,0)-- +(0.5,0) [->] node[midway,below] {$\vec{v}_2$}; \draw[opacity=0,line width=0.21mm] (-0.27,-0.30) rectangle (2.72,2); \end{tikzpicture}$$
Пусть в точке A носители заряда имеют скорость $$v_1$$. На участке AB за счет работы электрического поля их скорость растет до величины $$v_2$$. Одновременно с этим снижается плотность носителей заряда, чтобы величина тока $$I=jS=qnvS$$ оставалась постоянной: $$n_1v_1=n_2v_2$$. Далее носители движутся с постоянной скоростью до точки C, замедляются до $$v_1$$ к точке D и возвращаются на этой скорости в точку A.
В нерелятивистском случае, когда импульс одного носителя заряда есть $$p=mv$$, полный импульс носителей на участках BC и AD равен
$$P_\text{нерел}=mv_2n_2Sl-mv_1n_1Sl=0.$$
Но если учесть релятивистские эффекты, когда $$p=\gamma mv$$,
$$P_\text{рел}=\gamma_2mv_2n_2Sl-\gamma_1mv_1n_1Sl=(\gamma_2-\gamma_1){mIl\over q}.$$
Разность кинетической энергии $$K=\gamma mc^2$$ носителей на этих участках определяется работой электрического поля:
$$\gamma_2 mc^2-\gamma_1 mc^2=qEh.$$
Таким образом,
$$P_\text{скр}={IlEh\over c^2}={\mu E\over c^2},$$
где $$\mu$$ — магнитный момент витка с током.
Результат легко обобщается на случай произвольного точечного магнитного диполя в неоднородных электрических полях. Электрическое поле, перпендикулярное плоскости витка, не влияет на движение зарядов. Переходя от проекции электрического поля на плоскость витка к вектору, получаем
$$\vec{P}_\text{скр}={1\over c^2}\,\vec\mu\times\vec{E}.$$
Можно показать, что электромагнитный импульс в системе из заряда q и диполя $$\mu$$ определяется формулой
$$\vec{P}_\text{эм}=-{1\over c^2}\vec\mu\times\vec{E},$$
где $$\vec{E}=q\vec{R}/R^3$$ — электрическое поле заряда в точке, где находится диполь. Электромагнитный импульс полностью компенсируется скрытым импульсом. Мы не будем делать расчет конкретно для этой системы. Вместо этого покажем, что такая компенсация происходит всегда.
Скрытый импульс и импульс электромагнитного поля
В произвольном электростатическом поле с потенциалом $$\varphi$$ выражение для скрытого импульса витка с током I приобретает вид
$$\vec{P}_\text{скр}=-{I\over c^2}\oint\varphi\,d\vec{l}.$$
Если задана объемная плотность тока $$\vec{j}$$, то
$$\vec{P}_\text{скр}=-{1\over c^2}\int\varphi\vec{j}\,dV.$$
Подставим в последнюю формулу уравнение Максвелла для стационарных полей $$\nabla\times\vec{B}=(4\pi/c)\vec{j}$$:
$$\begin{align*} \vec{P}_\text{скр}&=-{1\over 4\pi c}\int\varphi\,\nabla\times\vec{B}\,dV=-{1\over 4\pi c}\int\left(\nabla\times\varphi\vec{B}-\nabla\varphi\times\vec{B}\right)\,dV=\\ &={1\over 4\pi c}\oint\varphi\vec{B}\times d\vec{S}-{1\over 4\pi c}\int\vec{E}\times\vec{B}\,dV=-{1\over c^2}\int\vec{S}\,dV=-\vec{P}_\text{эм}. \end{align*}$$
Первое слагаемое — интеграл по бесконечно удаленной поверхности — для замкнутых ограниченных в пространстве систем равен 0. Таким образом, мы получили, что ненулевой полный электромагнитный импульс системы всегда компенсируется скрытым импульсом. Полный импульс покоящейся стационарной системы — нулевой.
Природа скрытого импульса
Скрытый импульс связан с механическим движением носителей зарядов. Масса носителей фигурировала в выводе, но сократилась в итоговом ответе.
Скрытый импульс имеет релятивистский характер. Если бы не поправки специальной теории относительности, скрытый импульс был бы нулевым.
Природа скрытого импульса зависит от самой системы. В рассмотренной выше модели скрытый импульс (и поток энергии) связан с ускорением зарядов. В модели тока заряженной несжимаемой жидкости скрытый поток энергии вызывается перепадом давления. Во вращающемся заряженном диэлектрике (например, в сфере) импульс и поток энергии запасен в движении участков с разным механическим напряжением.
$$\begin{tikzpicture}[scale=2.109,line width=0.21mm,draw=red,node distance=4cm] \draw [fill=red!10] circle (0.7); \draw (-120:.15) [->,thin,black] arc(240:-60:.15); \def\n{12} \foreach \s in {1,...,\n} \node at ({360/\n * (\s-1)}:0.6) {$+$}; \node[fill=red!10,draw,circle] at (0,-1.3) {$+$}; \draw (0,-0.844) node {$\text{растянуто}$}; \draw (0,0.82) node {$\text{сжато}$}; \draw[line width=5,draw=black!20] (2,-0.3)+(0,-0.5) arc (270:90:0.5) -- +(2,0) node[midway,above=0.05mm] {$\text{натяжение меньше}$} arc (90:-90:0.5) -- +(-2,0) node[midway,below=-0.1mm] {$\text{натяжение больше}$}; \draw[fill=green!10,draw=green!40!black] (2,-0.3) circle(0.46) +(2,0) circle(0.46); \draw (2,-0.3) +(-120:.1) [->,thin,black] arc(240:-60:.1); \end{tikzpicture}$$
Поток механической энергии в последнем случае аналогичен потоку энергии в ременной передаче. Нижняя половина ремня на рисунке справа перемещается от нагрузки к двигателю. Она натянута больше, чем верхняя. При этом поток механической энергии направлен к нагрузке.
В настоящих электромагнитах скрытого импульса нет
В примере из введения нельзя заменить тороидальный магнит на соленоид с током. Если намотать соленоид металлическим проводом, то ни скрытого импульса внутри него, ни электромагнитного импульса снаружи не будет.
Всё дело в экранировке внешнего электрического поля в металле. Перераспределение поверхностных зарядов приводит к тому, что поверхность идеального проводника становится эквипотенциальной, и интеграл от плотности скрытого импульса $$-\varphi\vec{j}$$ зануляется.
Также исчезает и электромагнитный импульс. Электрическое поле перпендикулярно эквипотенциальным поверхностям, а вектор Пойнтинга направлен по касательным к ним. Потоки энергии текут вдоль эквипотенциальных поверхностей и вынуждены быть замкнутыми.
Ненулевое сопротивление настоящих металлов приводит к падению потенциала вдоль проводника и попаданию части потока энергии внутрь. Энергия исходит из источника тока и перемещается к проводнику, в котором переходит в тепло. Такая система уже нестационарна. В ней энергия перемещается от одной части к другой, и полный импульс отличен от нуля.
Чтобы в системе появился и электромагнитный, и скрытый импульс, вместо электромагнита надо взять неметаллический источник магнитного поля. Скрытый импульс $$-\varphi\vec{j}$$ будет запасен в молекулярных токах Ампера.
Критика скрытого импульса
Понятие скрытого импульса часто подвергается критике недостаточно компетентными авторами. Рассмотрим распространенные ошибки критиков на примере текста некоего Джеррольда Франклина.
-
В статье рассуждения начинаются не с вектора Пойнтигна, выражение для которого выводится из принципа наименьшего действия, а с применения третьего закона Ньютона к силе Лоренца. Начиная не с общих формул, а с частных, нельзя прийти к общим выводам.
-
Утверждается, что теорему о центре масс нельзя применить к электромагнитному полю, потому что взаимодействие с веществом $$-\vec{j}\cdot\vec{E}$$ нарушает равенство $$\partial_\mu T^{\mu\nu}_\text{эм}=0$$. Но правильно применять теорему к полной системе, включающей и электромагнитное поле, и вещество, а не к ее части.
-
Автор критикует модель витка с током, заявляя, что в ней появятся поверхностные заряды, компенсирующие внешнее электрическое поле. Аргумент имеет смысл только для систем с точной компенсацией зарядов разного знака вроде металлических проводников. Его легко обойти, потребовав, чтобы все заряды в витке были одного знака.
-
Еще одна грубая ошибка присутствует в предложении, по которому перераспределение зарядов по поверхности металлического проводника не приводит к исчезновению электромагнитного импульса. Суммарный ненулевой электромагнитный импульс присутствует в системе с ненулевым суммарным потоком электромагнитной энергии. Он появляется в системе с источниками и стоками энергии $$-\vec{j}\cdot\vec{E}\ne 0$$. Внутри и снаружи идеального проводника $$\vec{j}\cdot\vec{E}=0$$, электрическое поле существенно искажается и суммарный электромагнитный поток энергии исчезает.
-
Неверный логический переход в следующем выводе: во вращающихся диэлектрических заряженных телах не может быть ускорения носителей зарядов и связанной релятивистской добавки, и поэтому в ней нет скрытого импульса. На самом деле скрытый импульс есть, он имеет другую природу и связан с механическим напряжением, как мы показали выше.
Автору не удалось показать ни неприменимость теоремы о центре масс, ни отсутствие необходимости во введении понятия скрытого импульса, ни отсутствие самого скрытого импульса.
Круговая трактриса
Я люблю задачки, в которых нужно искать траектории частиц или уравнения необычных линий. К сожалению, они не всегда решаются аналитически. Разберем задачу, у которой аналитическое решение существует.
Задача
По окружности небольшого радиуса едет трактор. К нему на жестком стержне прикреплен груз (например, прицеп). По какой траектории будет двигаться груз?
При движении трактора по прямой траектория груза известна — это трактриса. В нашем случае движение будет более сложным. Я сделал анимацию искомой траектории — круговой трактрисы. Посмотрите на эту красоту.
Решение
Будем считать трактор точкой, движущейся по окружности радиуса r, и обозначать на рисунках зеленым кружком. К нему с помощью стержня длины L прикреплен груз (красный кружок).
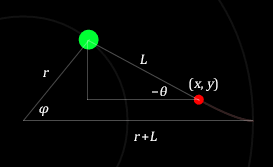
Из кинематических связей координаты груза определяются формулами
$$x=r\cos\varphi+L\cos\theta,\quad y=r\sin\varphi+L\sin\theta.$$
Еще одна кинематическая связь дает ограничение на скорость груза. По условию вектор скорости всегда направлен на трактор. Поэтому угол θ в прямоугольном треугольнике совпадает с точностью до знака с углом наклона касательной:
$${dy\over dx}=\text{tg\,}\theta.$$
Мы выразим θ через φ и получим уравнение траектории в параметрической форме. Введем новый параметр β = L/r, возьмем дифференциалы первых двух уравнений и подставим в последнее:
$$-{\cos\varphi\,d\varphi+\beta\cos\theta\,d\theta\over \sin\varphi\,d\varphi+\beta\sin\theta\,d\theta}=\text{tg\,}\theta.$$
Приведя к общему знаменателю и воспользовавшись основным тригонометрическим тождеством и формулой косинуса разности, получаем дифференциальное уравнение
$$\beta{d\theta\over d\varphi}+\cos(\theta-\varphi)=0.$$
Оно решается разделением переменных после замены θ = α + φ. Решение имеет разный вид в зависимости от параметра β:
$$\theta(\varphi)=\left\{\begin{array}{l}\varphi-2\,\text{arctg}\left[\sqrt{\dfrac{\beta+1}{\beta-1}}\,\text{tg}\left(\varphi\,\dfrac{\sqrt{\beta^2-1}}{2\beta}\right)\right],\quad\beta>1,\\\vphantom{\dfrac{1}{1}}\varphi-2\,\text{arctg}\,\varphi,\quad\beta=1,\\\varphi-2\,\text{arctg}\left[\sqrt{\dfrac{1+\beta}{1-\beta}}\,\text{th}\left(\varphi\,\dfrac{\sqrt{1-\beta^2}}{2\beta}\right)\right],\quad\beta<1.\end{array}\right.$$
Анализ решения
Если β < 1, движение непериодическое. Груз следует за трактором, асимпотически приближаясь к окружности. Интересный режим возникает при β = 1. Тогда груз неограниченно приближается к центру окружности:
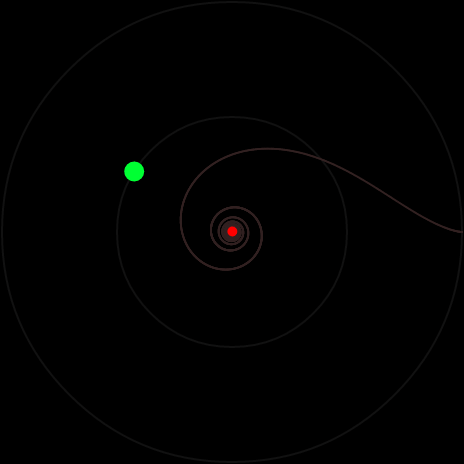
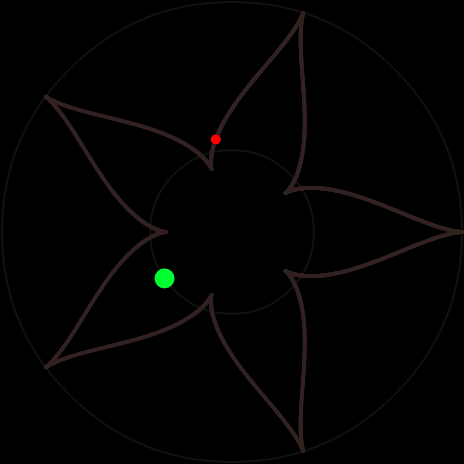
Если β > 1, движение будет периодическим по звездообразной траектории:
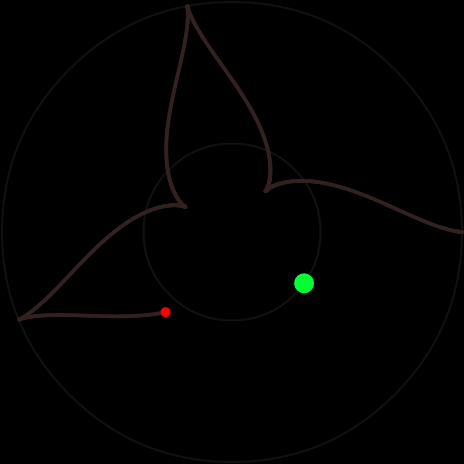
Чтобы найти угол между направлениями на соседние максимум и минимум, заметим, что груз находится дальше всего от центра, когда θ и φ совпадают, и ближе всего к центру, когда отличаются на π. В первом случае тангенс равен нулю, во втором — расходится. Возьмем направление на максимум θ = φ = 0 и направление на первый минимум φ = θ + π, определяющийся условием
$$(\pi+\theta)\,{\sqrt{\beta^2-1}\over 2\beta}={\pi\over 2}.$$
Угол между направлениями составляет
$$\theta=\pi\left({\beta\over\sqrt{\beta^2-1}}-1\right).$$
Если параметр удовлетворяет условию
$${1\over N}={\beta\over\sqrt{\beta^2-1}}-1,$$
то груз описывает замкнутую линию — N-конечную звезду. Вот пример для $$N=5,\beta=6/\sqrt{11}$$:
Торможение реликтовым излучением
На втором курсе за неделю перед досрочным экзаменом по теоретической физике Семен Соломонович Герштейн задал мне две задачи. В одной требовалось найти угловое распределение синхротронного излучения электрона, движущегося по окружности. Вторая оказалась интереснее: найти силу торможения со стороны реликтового излучения на площадку, движущуюся перпендикулярно самой себе. Остановимся на ней подробнее. Записей с тех времен у меня не сохранилось, а в литературе опубликованы противоречивые результаты. Хороший повод заново разобраться в задаче.
Обозначения и соглашения
Под реликтовым излучением мы подразумеваем равновесное тепловое излучение при некоторой температуре T. Напомним, что плотность энергии и давление равновесного излучения определяются температурой: ε = 4πσT4/c, P = ε/3.
В системе отсчета, связанной с реликтовым излучением, оно однородно и изотропно. Относящиеся к ней величины будем обозначать символами без штрихов. Относительно этой системы со скоростью v движется площадка (например, диск) с коэффициентом отражения R. Штрихами обозначим величины в сопутствующей системе отсчета (связанной с площадкой).
Будем опускать скорость света c в тех формулах, где она легко восстанавливается из соображений размерности.
Обзор литературы
В публикациях по этой проблеме нет консенсуса. Например, в письме Андрея Шепелева в УФН под названием «Космический микроволновой фон и аристотелевы представления о движении» приведена формула для давления на площадку $$P=-v\,(1+v^2/2)\,\varepsilon/2$$. Этот ответ, как мы увидим ниже, явно ошибочен. Автор не раскрывает вычислений, поэтому невозможно понять, где ошибка.
В работе Баласаняна и Мкртчяна «Blackbody radiation drag on a relativistically moving mirror» вычисляется плотность импульса в системе отсчета, связанной с диском, и она отождествляется с давлением (с точностью до учета отражения). По поводу этой работы у меня есть два замечания.
$$n'(\vec{k}')={1\over e^{\gamma(\omega' +k'_xv)/T}-1}.$$(1)
В то же время плотность импульса электромагнитного излучения отличается на множитель 1/c2 от вектора Поинтинга, проекции которого есть компоненты T0i тензора
$$T^{\mu\nu}=\begin{pmatrix}\varepsilon &0&0&0\\0&\varepsilon/3&0&0\\0&0&\varepsilon/3&0\\0&0&0&\varepsilon/3\end{pmatrix},$$
сразу получаем плотность импульса (см. II том Ландау и Лифшица, §35, формула 35.3)
$$S'_x=-{4\over 3}\,\varepsilon\,{v\over 1-v^2}.$$(2)
Вычисление в сопутствующей системе отсчета
$$\usetikzlibrary{decorations.pathmorphing} \begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small \tikzset{>=stealth} \tikzset{snake it/.style={->,semithick, decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate}} \def\h{3} \def\d{0.2} \def\ww{1.4} \def\w{1+\ww} \def\p{1.5} \def\r{0.7} \coordinate[label=below:$A$] (A2) at (\w,\p); \coordinate[label=above:$B$] (B2) at (\w,\p+\h); \coordinate[label=left:$C$] (C1) at (0,0); \coordinate[label=left:$D$] (D) at (0,\h); \draw[fill=blue!14](A2)--node[left]{$S$}(B2)-- ++(\d,0)-- ++(0,-\h)--cycle; \draw[gray,thin](C1)-- +(\w+\d,0); \draw[dashed,line width=0.2mm](C1)--(D); \draw[snake it](C1)--(A2) node[pos=0.5,above,inner sep=8] {$c\Delta t$}; \draw[snake it](D)--(B2); \draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$}; \draw[opacity=0](-0.40,-0.14)-- ++(0,5.06); \end{tikzpicture}$$Давление как силу на единицу поверхности определим через импульс, передаваемый диску при отражении или поглощении фотонов за единицу времени:
$$P={F\over S}={1\over S}{\hbar\Delta k\over\Delta t}.$$
Если фотоны летят под углом θ к нормали, то за время Δt до неподвижной площадки S долетят фотоны из объема S cΔt |cos θ|. Из них доля R отразится и доля (1−R) поглотится. Каждый поглощенный фотон отдаст импульс $$\hbar k\cos\theta=\hbar\omega\cos\theta/c$$, а каждый отраженный — в два раза больше. Собирая всё вместе, получаем в сопутствующей системе отсчета
$$P=\int{\hbar\omega'\cos\theta'\over S\,c\Delta t'}\,(1+R)\,S\,c\Delta t'\,|\cos\theta'|\,n'(\vec{k}')\,d^3k'.$$
Напомним, что частота ω и волновой вектор $$\vec{k}$$ образуют четырехвектор $$(\omega, \vec{k})$$. Переход к движущейся системе координат осуществляется преобразованиями Лоренца
$$\omega'={\omega-k_xv\over\sqrt{1-v^2}},\qquad k_x'={k_x-\omega v\over\sqrt{1-v^2}}.$$
Функция распределения $$n(\vec{k})$$ в фазовом пространстве инвариантна относительно преобразований Лоренца, так как и элемент фазового объема $$d^3r\,d^3k$$, и число частиц $$dN=n(\vec{r},\vec{k})\,d^3r\,d^3k$$ есть инварианты (подробнее см. II том Ландау и Лифшица, §10). Именно поэтому функция распределения в движущейся системе $$n'(\vec{k'})=n(\vec{k})$$ есть обычное распределение Бозе — Эйнштейна (1), в которое подставлена преобразованная частота.
В итоге давление определяется следующим интегралом
$$P=\int \hbar\omega'\cos\theta'\,(1+R)\,|\cos\theta'|\,{const\over exp\left(\dfrac{\hbar\omega'}{kT}\,\dfrac{1+v\cos\theta'}{\sqrt{1-v^2}}\right)-1}\,\omega'^2\,d\omega'\,{d(\cos\theta')\over 2}.$$(3)
Вместо того чтобы следить за комбинацией констант, которая в итоге должна свестись к постоянной
$$\varepsilon=\int \hbar\omega\,{const\over exp\left(\dfrac{\hbar\omega}{kT}\right)-1}\,\omega^2\,d\omega={4\pi\sigma\over c}T^4.$$
Еще отсюда видно, что (3) можно упростить, проинтегрировав по частотам. Множитель $${\sqrt{1-v^2}}/{(1+v\cos\theta')}$$ перед температурой в экспоненте появится под интегралом в четвертой степени. Дальнейшее вычисление тривиально:
$$P=\varepsilon\,(1+R)\int\limits_{-1}^{1}\cos\theta'\,|\cos\theta'|\,\dfrac{(1-v^2)^2}{(1+v\cos\theta')^4}\,{d(\cos\theta')\over 2},$$
$${\Large\boxed{P=-\varepsilon\,(1+R)\,\frac{v\,(1+v^2/3)}{1-v^2}}.}$$(4)
Чтобы убедиться в правильности результата, вычислим тем же методом давление фотонного газа на одну сторону покоящейся пластины. Зависящий от скорости подынтегральный множитель исчезает, а интеграл в пределах от 0 до 1 равен 1/3. Полное давление есть (1+R) ε/6. Если пластина всё отражает и ничего не поглощает, давление совпадает с ожидаемой величиной ε/3. Если пластина всё поглощает, давление равно ε/6 и составляет половину от давления фотонного газа ε/3. Вторая половина набегает за счет собственного излучения пластины, которое мы в наших расчетах не учитывали.
Формула (4) не совпадает ни с результатом Шепелева, который утверждает, что ответ сложен, и раскладывает его в ряд, ни с результатом Баласаняна, который ошибочно отождествляет в этой задаче плотность импульса и давление.
Вычисление в неподвижной системе отсчета
$$\usetikzlibrary{decorations.pathmorphing}
\begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small
\tikzset{>=stealth}
\tikzset{snake it/.style={->,semithick,
decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate}}
\def\h{3}
\def\d{0.2}
\def\ww{1.4}
\def\w{1+\ww}
\def\p{1.5}
\def\r{0.7}
\coordinate[label=below:$A_1$] (A1) at (\ww,\p);
\coordinate[label=above:$B_1$] (B1) at (\ww,\p+\h);
\coordinate[label=below:$A_2$] (A2) at (\w,\p);
\coordinate[label=above:$B_2$] (B2) at (\w,\p+\h);
\coordinate[label=left:$C$] (C1) at (0,0);
\coordinate[label=left:$D$] (D) at (0,\h);
\draw[fill=blue!14](A2)--(B2)-- ++(\d,0)-- ++(0,-\h)--cycle;
\draw[gray,thin](C1)-- +(\w+\d,0);
\draw[dashed,gray,fill=blue!5](A1)-- (B1)-- ++(\d,0)-- ++(0,-\h)-- cycle;
\draw[dashed,line width=0.14mm](A1)--(C1)--(D)--(B1);
\draw[snake it](C1)--(A2) node[pos=0.6,below] {$c\Delta t$};
\draw[->,semithick](\ww,\p+0.44*\h)-- +(\w-\ww,0) node[pos=0.6,above] {$v\Delta t$};
\draw[snake it](D)--(B2);
\draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$};
\draw[opacity=0](-0.40,-0.14)-- ++(0,5.06);
\end{tikzpicture}$$
Тот же результат получается и в неподвижной системе отсчета. В ней не нужно иметь дела с функцией распределения фотонов, однако
Чтобы понять, сколько летящих под углом θ фотонов с частотой ω попадет за время Δt на площадку AB, нужно ввести понятие «заметаемого объема» (объем, фотоны из которого попадут на диск) и умножить его величину на плотность фотонов nω. За это время площадка переместится из положения A1B1 в положение A2B2, а фотоны из точек C и D долетят до диска. Таким образом, заметаемый объем соответствует фигуре A1B1DС, и его величина равна S |cΔt cos θ − vΔt|.
При отражении фотона от площадки в сопутствующей системе отсчета знак проекции волнового вектора фотона изменяется на противоположный: $$k'_{2x}=-k'_{1x}$$. Найдем соответствующее изменение в неподвижной системе:
$$\begin{aligned}\Delta k &=k_{1x}-k_{2x}=k_{1x}-\gamma(k'_{2x}+\omega'_2v)=k_{1x}+\gamma(k'_{1x}-\omega'_1v)=\\&=k_{1x}+\gamma\left(\gamma(k_{1x}-\omega_1 v)-\gamma(\omega_1-k_{1x}v)v\right)=k_{1x}+\gamma^2\left(k_{1x}(1+v^2)-2v\omega\right).\end{aligned*}$$
Выражая проекцию волнового вектора через частоту фотона и азимутальный угол $$k_x=\omega\cos\theta$$, получаем
$$\Delta k=\omega\left[\cos\theta\left(1+{1+v^2\over 1-v^2}\right)-2{v\over 1-v^2}\right]={2\omega\over 1-v^2}\,(\cos\theta-v).$$
Ясно, что двойку в последнем выражении нужно заменить на (1+R), чтобы учесть случай произвольного коэффициента отражения R. Давление
$$P_\omega=\int{\hbar\omega\over S\,c\Delta t}\,{1+R\over 1-v^2}\,(\cos\theta-v)\,S|c\Delta t\cos\theta-v\Delta t|\,n_\omega\,{d(\cos\theta)\over2},$$
$$P_\omega={n_\omega\over 2}\hbar\omega\,{1+R\over 1-v^2}\int\limits_{-1}^{1}dx\,(x-v)|x-v|.$$
После вычисления интеграла и усреднения плотности энергии $$n_\omega\hbar\omega$$ по частотам получается формула (4).