Метод наименьших квадратов во многомерном пространстве

Я собираюсь применить метод наименьших квадратов для проведения гиперплоскости через набор точек во многомерном пространстве. Для начала вспомним суть метода и поймем, в чем состоит задача.

В простейшем случае метод наименьших квадратов применяется для проведения прямой линии через набор экспериментальных точек и состоит в минимизации суммы квадратов отклонений $$\inline\sum(y_i-ax_i-b)^2$$, которые списываются на погрешность измерений. В результате минимизации для коэффициентов a и b получается простая система линейных уравнений. Здесь важно предположение о том, что ошибки по оси x пренебрежимо малы по сравнению с ошибками по оси y. Если это не так, то минимизировать нужно более сложное выражение.

Иногда возникает задача другого рода — провести геометрическую прямую через набор геометрических точек «наилучшим образом». Для этой задачи метод наименьших квадратов нужно адаптировать, так как поспешное применение формул для коэффициентов a и b будет давать разные прямые в разных системах координат. Теперь отклонения по осям должны быть одинаковы. Правильный подход заключается в минимизации суммы квадратов расстояний $$\inline\sum(y_i-ax_i-b)^2/(1+a^2)$$ от точек (x_i, y_i) до проводимой прямой. Он дает нелинейную систему уравнений, которую можно решать численно. Однако этот подход тяжело обобщается на интересующий меня многомерный случай. Поэтому мы с самого начала будем рассматривать задачу во многомерном пространстве.

Задача

Пусть задан набор точек $$\vec{x}^k$$. Мы хотим провести гиперплоскость $$(\vec{n}\cdot\vec{x}) = d$$ такую, что сумма квадратов расстояний от точек $$\vec{x}^k$$ до нее будет минимальна. Расстояние до гиперплоскости находится с помощью проекции на единичный вектор нормали $$\vec{n}$$, и выражение для минимизации принимает вид

$$\sum_k\left((\vec{n}\cdot\vec{x}^k)-d\right)^2\to\text{min}.$$

При этом нужно учитывать уравнение связи $$(\vec{n}\cdot\vec{n}) = 1$$, которое уменьшает на 1 количество степеней свободы в неизвестных величинах n_i, d. Учет связи выполняется с помощью метода множителей Лагранжа. Однако мы пойдем другим путем, который сократит выкладки и напрямую приведет к выражениям, подходящим для численного счета. Мы разрешим вектору $$\vec{n}$$ иметь произвольную длину, и введем явную нормировку:

$$\sum_k\left({(\vec{n}\cdot\vec{x}^k)\over|\vec{n}|}-d\right)^2\to\text{min}.$$

Параллельный перенос

Продифференцируем по d:

$$\sum_k\left({(\vec{n}\cdot\vec{x}^k)\over|\vec{n}|}-d\right)={(\vec{n}\cdot\sum_k\vec{x}^k)\over|\vec{n}|}-\sum_kd=0.$$

Как видим, «центр масс» набора точек $$\inline\sum\vec{x}^k/\sum 1$$ находится на искомой плоскости. Выполним параллельный перенос системы координат таким образом, чтобы ее начало совпало с центром набора точек $$\inline\sum\vec{x}^k=0$$. В этой системе координат d=0.

Условие на вектор нормали

Перейдем к индексным обозначениям и продифференцируем по n_a:

$${\partial\over\partial n_a}\left({n_ix_i^k\,n_jx_j^k\over n_ln_l}\right)={2x_a^k\,n_jx_j^k\over n_ln_l}-{2n_a\,n_ix_i^k\,n_jx_j^k\over n_ln_l\,n_pn_p}=0,$$

$$n_jx_j^k\left[x_a^k(n_pn_p)-n_a(n_ix_i^k)\right]=0,$$

$$\sum_k\vec{n}\cdot\vec{x}^k\left[\vec{x}^k(\vec{n}\cdot\vec{n})-\vec{n}(\vec{n}\cdot\vec{x}^k)\right]=0.$$

Вычислительный аспект

Нелинейное уравнение относительно вектора $$\vec{n}$$ можно решать методом итераций:

$$\sum_k\vec{n}_{i+1}\cdot\vec{x}^k\left[\vec{x}^k(\vec{n}_i\cdot\vec{n}_i)-\vec{n}_i(\vec{n}_i\cdot\vec{x}^k)\right]=0.$$

С помощью матрицы $$A_{aj}(\vec{n})=\left[x_a^k(n_pn_p)-n_a(n_ix_i^k)\right]x_j^k$$ оно представляется в виде

$$A(\vec{n}_i)\,\vec{n}_{i+1}=0$$

и сводится к поиску ядра линейного оператора. Нетривиальность ядра связана с «лишней» степенью свободы, появившейся из-за отбрасывания условия нормировки вектора нормали. Читатели могут самостоятельно проверить с помощью формулы Бине — Коши, что определитель матрицы $$A(\vec{n}_i)$$ равен нулю.

По теореме Фредгольма ядро оператора ортогонально образу сопряженного оператора, то есть линейной оболочке, натянутой на строки $$\vec{a}_a$$ матрицы $$A_{aj}(\vec{n}_i)$$. Алгоритм поиска ортогонального дополнения состоит в выборе произвольного вектора $$\vec{r}$$ и ортогонализации набора векторов $$\vec{r}, \vec{a}_a$$:

$$\vec{r}^{\,\prime}=\vec{r}-\vec{a}_1{(\vec{r}\cdot\vec{a}_1)\over(\vec{a}_1\cdot\vec{a}_1)},$$

$$\vec{a}_2^{\,\prime}=\vec{a}_2-\vec{a}_1{(\vec{a}_2\cdot\vec{a}_1)\over(\vec{a}_1\cdot\vec{a}_1)},\quad\vec{r}^{\,\prime\prime}=\vec{r}^{\,\prime}-\vec{a}_2^{\,\prime}{(\vec{r}^{\,\prime}\cdot\vec{a}_2^{\,\prime})\over(\vec{a}_2^{\,\prime}\cdot\vec{a}_2^{\,\prime})}\ldots$$

Так как строки матрицы $$A(\vec{n}_i)$$ линейно зависимы, один из векторов $$\vec{a}_a$$ при ортогонализации из набора исключается. Для большей определенности алгоритма в качестве начального приближения перебираем базисные векторы, пока в результате ортогонализации не получится ненулевой вектор следующего приближения $$\vec{n}_{i+1}$$. В двумерном и трехмерном случае процесс ортогонализации значительно упрощается. Например, в трехмерном случае нетривиальный элемент ядра найдется среди тройки векторов $$\vec{a}_1\times\vec{a}_2, \vec{a}_1\times\vec{a}_3, \vec{a}_2\times\vec{a}_3$$.

Как показывают практические вычисления, последовательные приближения $$\vec{n}_i$$ быстро сходятся к искомому вектору нормали.

Магнитные монополи, потоки энергии и квантование заряда

Мы уже рассчитывали замкнутые потоки энергии в стационарных полях зарядов и магнитов. Перейдем к более экзотическому примеру с участием не открытого на опыте магнитного монополя.

Как и в любых скрещенных электрических и магнитных полях, вокруг электрического заряда и магнитного монополя существуют потоки энергии, определяемые вектором Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$. Они замкнуты и охватывают ось симметрии системы, что может означать наличие в ней момента импульса.

Если заряд движется строго на монополь, то взаимодействие между ними отсутствует. Действительно, монополь не испытывает действие электрического поля заряда. Магнитное поле заряда на линии движения нулевое. Монополь не создает электрическое поле, а его магнитное поле коллинеарно скорости заряда, поэтому силы на заряд тоже не действуют. Отсутствие взаимодействия в этом случае наводит на мысль о том, что момент импульса остается неизменным.

По соображениям размерности момент импульса, как безразмерная величина (в единицах c = ħ = 1), не может зависеть от расстояния между зарядом и монополем — единственного размерного параметра системы. Убедимся в этом непосредственным вычислением.

Поместим электрический заряд q в точку $$\vec{a}$$ и магнитный заряд m в точку $$-\vec{a}$$. Тогда они будут создавать поля

$$\vec{E}(\vec{R})={q\over |\vec{R}-\vec{a}|^3}(\vec{R}- \vec{a}),\quad\vec{B}(\vec{R}) ={m\over |\vec{R} + \vec{a}|^3}(\vec{R} + \vec{a}).$$

Плотность импульса связана с вектором Пойнтинга

$$\vec{P} = {\vec{S} \over c^2} = {1\over 4\pi c}\vec{E}\times\vec{B}= {qm\over 4\pi c}{(\vec{R}-\vec{a})\times (\vec{R}+\vec{a})\over \left(\left(R^2+a^2\right)^2-4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$

Полный момент импульса находится интегрированием по всему пространству

$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV={qm\over 2\pi c}\int\! dV{\vec{R}\times[\vec{R}\times\vec{a}]\over \left(\left(R^2 + a^2\right)^2- 4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$

Выбираем ось z вдоль $$\vec{a}$$, угол между этой осью и радиус-вектором $$\vec{R}$$ есть полярный угол θ. Из соображений симметрии момент импульса должен быть направлен по оси z. Раскрываем двойное векторное произведение, находим проекцию на z и сразу интегрируем по азимутальному углу φ

$$L_z={qm\over c}\int\limits_0^{\infty}\! R^2dR\int\limits_{-1}^{1}\! d(\cos\theta){-a\,R^2\sin^2\theta\over \left(\left(R^2 + a^2\right)^2- 4(R\,a\cos\theta)^2\right)^{3/2}}.$$

Разделим числитель и знаменатель на a⁶ и введем новую безразмерную переменную интегрирования r = R/a. Таким образом, мы избавились от явной зависимости момента импульса от расстояний. Двойной интеграл не зависит от параметров задачи. С помощью любимого математического пакета можно убедиться, что он равен 1.

$$L_z=-{qm\over c}\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! d(\cos\theta){1-\cos^2\theta\over \left(\left(r^2 + 1\right)^2- 4r^2\cos^2\theta\right)^{3/2}}=-{qm\over c}.$$

Таким образом, момент импульса в системе заряда и монополя направлен к последнему и равен (с точностью до несущественного множителя c) произведению их величин.

В квантовой механике момент импульса квантуется. Из полуклассических соображений приравнивая полученное выше выражение для момента к минимальному значению ħ/2, мы получаем такое же ограничение на минимальные («элементарные») значения электрического и магнитного зарядов, как и в теории Дирака (где ограничение следует из дискретности прироста фазы волновой функции заряда при полном обороте вокруг монополя)

$$q_{min}\, m_{min}={\hbar c\over 2}.$$

Как видим, присутствие во Вселенной хотя бы одного монополя приводит к квантованию всех электрических зарядов.

Поиски бозона Хиггса на LHC

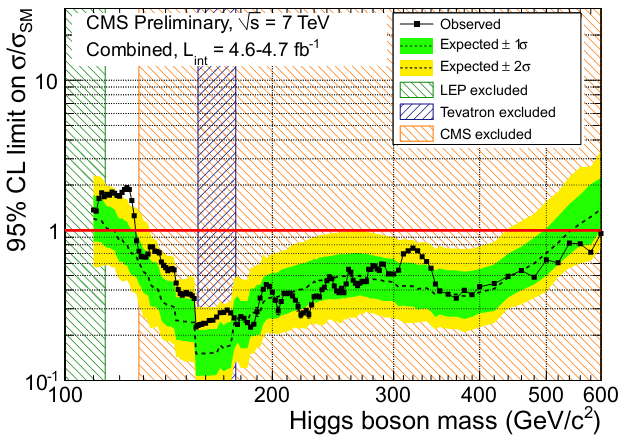
Сегодня в ЦЕРНе состоялся доклад коллабораций ATLAS и CMS, на котором были представлены предварительные результаты обработки данных, набранных в 2011 году. CMS уже исключил хиггсовский бозон стандартной модели в диапазоне масс от 128 до 600 ГэВ. С учетом ограничений, полученных на LEP, разрешенным является диапазон от 115 до 128 ГэВ. Он сейчас не закрыт из-за избытка событий, наблюдающегося в нескольких каналах.

 

Именно там, на энергии в 126 ГэВ, ATLAS наблюдает пик в одном из возможных каналов распада (локально 3,6σ, глобально 2,3σ).

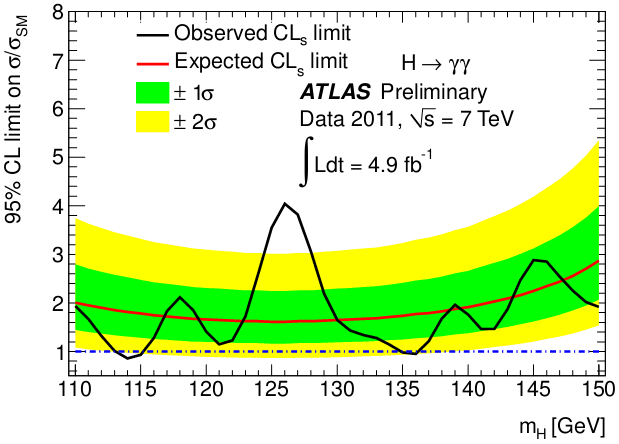
Если бозон Хиггса действительно существует, он должен проявляться в данных именно так. Но в то же время подобное превышение может оказаться случайным выбросом фоновых событий. Для полноценного открытия нужно превышение сигнала над ошибками в 5σ.

Доклад завершился словами о том, что хиггсовский бозон пока и не открыт, и не исключен.

Простейшая модель электрона: электромагнитная масса и гиромагнитное отношение

Продолжим развлекаться с классической электродинамикой. В прошлый раз мы подсчитали момент импульса в системе, состоящей из магнитного момента (маленькой катушки) в центре большой равномерно заряженной сферы

$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$(1)

Но магнитное поле вокруг сферы можно создать без дополнительной катушки, просто закрутив ее. Получается, что часть момента импульса вращающейся сферы запасается в ее электромагнитном поле. Определим эту добавку.

Магнитный момент вращающейся сферы 

Мы собираемся показать, что магнитное поле вне равномерно заряженной сферы радиуса a и заряда Q, вращающейся с угловой скоростью ω, точно совпадает с полем магнитного диполя.

Начинаем с векторного потенциала

$$\vec{A}={1\over c}\int\!{\vec{j}\over r}\,dV={Q\over 4\pi ca^2}\int\!{\vec{v}\over r}\,dS={Q\over 4\pi ca^2}\int\!{\vec{\omega}\times a\vec{n}\over r}\,dS,$$

где $$r=|\vec{R}-a\vec{n}|$$ — расстояние от элемента поверхности dS, задаваемого радиус-вектором $$a\vec{n}$$, до точки $$\vec{R}$$, в которой вычисляется векторный потенциал. Учитывая линейность векторного произведения, получаем

$$\vec{A}={Q\over 4\pi ca}\,\vec{\omega}\times\int\!{\vec{n}\over \sqrt{R^2 + a^2-2Ra\cos\chi}}\,dS={Q\over 4\pi ca}\,\vec{\omega}\times\vec{I}.$$

Интеграл $$\vec{I}$$ в последнем выражении — это усреднение единичного вектора $$\vec{n}$$ по направлениям с весом 1/r. Исходя из соображений симметрии ясно, что в результате интегрирования мы получим вектор, параллельный вектору $$\vec{R}$$. Подтвердим это вычислением.

В сферических координатах $$\inline \vec{n}=(\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)$$. Направим вектор $$\vec{R}=(0,0,R)$$ вдоль оси z. Тогда угол χ между векторами $$\inline \vec{n}$$ и $$\inline \vec{R}$$ совпадает со сферической координатой θ. Z-компонента интеграла

$$I_z=a^2\int\!\cos\theta\,{1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}\,d(\cos\theta)\,d\varphi.$$

Известно, что функцию 1/r можно разложить по многочленам Лежандра (нас интересует область R > a)

$${1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}=\sum\limits_{l=0}^\infty{a^l\over R^{l+1}}P_l(\cos\theta).$$

Подынтегральное выражение состоит из произведения этого ряда на многочлен Лежандра $$P_1(\cos\theta)=\cos\theta$$. Тогда из условия ортогональности

$$\int\limits_{-1}^{1} P_k(x)P_l(x)\,dx={2\over 2k+1}\delta_{kl}$$

сразу следует ответ

$$I_z={4\pi\over 3}{a^3\over R^2}.$$

Компоненты I_x и I_y пропорциональны интегралам от периодических функций sin φ и cos φ, и поэтому равны нулю. Переходя от проекций к вектору, для векторного потенциала получаем

$$\vec{A}={Qa^2\over 3c}\,\vec{\omega}\times{\vec{R}\over R^3}.$$

Таким образом, магнитное поле вне вращающейся сферы совпадает с полем магнитного диполя

$$\vec{\mathfrak{m}}={Qa^2\vec{\omega}\over 3c}.$$(2)

Для полноты отметим, что аналогичными вычислениями легко показать однородность магнитного поля внутри вращающейся сферы.

Электромагнитная масса

Коэффициент в (1) можно переписать по-другому, если ввести понятие электромагнитной массы. Оно подробно разбирается в главе 28 выпуска 6 фейнмановских лекций (ниже мы воспроизводим некоторые вычисления оттуда и фактически на протяжении двух постов разбираем задачу 2 к этой главе).

Вслед за Фейнманом мы будем называть электромагнитной массой коэффициент пропорциональности между скоростью равномерного движения сферы и импульсом электромагнитного поля. В нерелятивистском случае

$$\vec{E}=Q{\vec{R}\over R^3},\quad\vec{H}={Q\over c}{\vec{v}\times\vec{R}\over R^3}.$$

Тогда импульс электромагнитного поля дается интегралом

$$\vec{P}={1\over 4\pi c}\int\!\vec{E}\times\vec{H}\,dV={Q^2\over 4\pi c^2}\int\!{1\over R^4}\,\vec{n}\times\left[\vec{v}\times\vec{n}\right]\,dV.$$

Такой интеграл (с точностью до коэффициента) мы вычисляли в прошлый раз, поэтому сейчас просто выпишем ответ

$$\vec{P}={2Q^2 \over 3 ac^2}\,\vec{v}=m_e \vec{v}.$$

Гиромагнитное отношение и модель электрона

Теперь мы можем переписать (1) в таком виде

$$\vec{L}={m_ec\over Q}\,\vec{\mathfrak{m}}.$$

Мы получили интересный результат: гиромагнитное отношение для вращающейся безмассовой заряженной сферы совпадает с гиромагнитным отношением электрона.

Обычно в литературе по квантовой механике утверждается, что нельзя представлять себе спин электрона как его вращение, так как в такой модели скорость точек на его поверхности будет больше скорости света. Сейчас мы в этом убедимся.

Подставим в (1) магнитный момент (2) и спин электрона ½:

$${\hbar\over 2}={2\over 3}\,{Q\over ca}\,{Qa^2\omega\over 3c},$$

откуда отношение экваториальной скорости к скорости света есть

$${a\omega\over c}={9\over 4}\,{\hbar c\over Q^2}={9\over 4\alpha}\approx308.$$

Несостоятельность простейшей модели электрона проявляется и в том, что полная энергия электрического поля

$$U={1\over 8\pi}\int\!{E^2}\,dV={1\over 8\pi}\int\limits_a^{\infty}{Q^2\over R^4}\,4\pi R^2\,dR={Q^2 \over 2a}={4\over 3}\,m_ec^2$$

отличается от ожидаемой величины m_ec².

Парадокс Фейнмана, или потоки энергии в постоянных электромагнитных полях

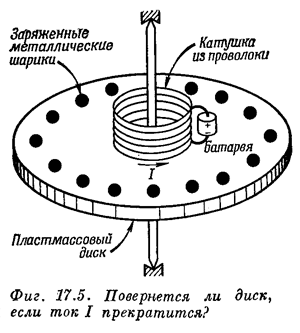
В фейнмановских лекциях по физике (выпуск 6, глава 17) есть описание следующего парадокса.

Представим, что мы конструируем прибор, в котором имеется тонкий круглый пластмассовый диск, укрепленный концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается. На диске имеется катушка из проволоки — короткий соленоид, концентричный по отношению к оси вращения. Через этот соленоид проходит постоянный ток I от маленькой батареи, также укрепленной на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одинаковым зарядом Q. Вся картина стационарна, и диск неподвижен.

Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без какого-либо вмешательства извне. Пока через соленоид шел ток, более или менее параллельно оси диска проходил магнитный поток. После того как ток прервался, поток этот должен уменьшиться до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружностям с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внешней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вращающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнет вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую скорость.

Но можно рассуждать и по-другому. Используя закон сохранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нулевым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернется ли диск или нет? Мы предлагаем вам подумать над этим вопросом.

Решение парадокса заключается в том, что в присутствии электрических и магнитных полей имеются потоки энергии, описываемые вектором Пойнтинга $$\vec{S} \sim \vec{E} \times \vec{B}$$. В предложенной Фейнманом конфигурации эти потоки замкнуты. Поскольку поток энергии однозначно связан с плотностью импульса, наличие замкнутых потоков энергии свидетельствует о присутствии ненулевого момента импульса. Таким образом, в системе изначально был запас момента импульса, который после исчезновения магнитного поля был передан диску.

Однако есть люди, которые убеждены в том, что выражение для вектора потока энергии через векторное произведение полей годится только для переменных электромагнитных полей (действительно, перенос энергии в этом случае можно увидеть непосредственно). Им не нравится, что, согласно выражению для вектора Пойнтинга, энергия течет от источника постоянного тока к нагрузке не «по проводам», а снаружи. Основной аргумент сводится к тому, что на поток энергии легко влияют манипуляции с проводом, наличие примесей, разрывов; в то время как никакими телами снаружи, например, дополнительными зарядами или магнитами, остановить поток энергии к нагрузке не удается.

Противники применения вектора Пойнтинга в статике придумывают в этом случае другие выражения для плотности энергии, например, $$\varphi \vec{j}$$. Но такое выражение тоже не лишено недостатков, приписываемых вектору Пойнтинга. Даже если отбросить требование единообразного описания явлений и попытаться применить для зарядов и катушки выражение $$\varphi \vec{j}$$, мы сразу столкнемся с тем, что потенциал φ в точках катушки (а, значит, и и момент импульса системы) легко изменить, поместив систему внутрь большого проводящего заряженного ящика и меняя его заряд. Это плохо согласуется с гипотезой, по которой энергия, как и ток, течет по катушке.

В связи с такой критикой вектора Пойнтинга можно заняться интересным упражнением — непосредственно вычислить момент импульса электромагнитного поля через вектор Пойнтинга и сравнить его с моментом импульса, передаваемым диску. Даже если критиков эти вычисления не убедят, мы еще раз увидим красоту теории.

$$\begin{tikzpicture}[x=(-30:3cm),y=(30:3cm),z=(90:3cm),>=stealth] \def\R{1} \draw[blue,->] (0,0,0) -- (0,0,0.3\R) node[right] {$\vec{\mathfrak{m}}$}; \draw[thin] (0,0,0) -- (.7\R,.7\R,0) node[below,pos=0.5] {$a$}; \node[orange!80!black] at (0,\R,0.5*\R) {$Q$}; \def\r{0.075} \draw[blue,->,thick] (\r,0,0) arc (0:360:\r); \foreach \i in {0, 30,...,150} \draw [orange!40!black,dotted] plot [domain=-180:180, samples=30, variable=\j] (\R*cos \i*sin \j,\R*sin \i*sin \j, \R*cos \j); \foreach \j in {0, 15,...,165} \draw [orange!40!black,dotted] plot [domain=0:360, samples=60, variable=\i] (\R*cos \i*sin \j,\R*sin \i*sin \j, \R*cos \j); \end{tikzpicture}$$

Для упрощения вычислений изменим систему, предложенную Фейнманом. Будем рассматривать не заряды на краю диска, а равномерно заряженную сферу радиуса a, в центре которой находится небольшая катушка, обладающая магнитным моментом $$\vec{\mathfrak{m}}$$. Магнитный момент, находящийся в начале координат, создает в точке $$\vec{R}$$ векторный потенциал

$$\vec{A} = {\vec{\mathfrak{m}} \times \vec{R} \over R^3}$$(1)

и магнитное поле

$$\vec{H} = {3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n})-\vec{\mathfrak{m}} \over R^3}, \quad \vec{n} = {\vec{R}\over R}.$$

$$\usetikzlibrary{arrows.meta,positioning,decorations.markings,backgrounds} \colorlet{EcolFL}{orange!80!black} \tikzset{EFieldLineArrow/.style={EcolFL,decoration={markings,mark=at position 1 with {\arrow{Stealth}}},postaction={decorate}}} \def\R{0.8} \def\NE{8} \begin{tikzpicture}[-,scale=6] \foreach \i [evaluate={\angle=(\i-1)*360/\NE;}] in {1,...,\NE}{ \draw[EFieldLineArrow] (\angle:0) -- (\angle:\R); } \node[draw=EcolFL,fill=white,circle, minimum size=4cm, inner sep=0, outer sep=0] (circ) at (0,0) {}; \node[EcolFL,right] at (0.56,0.56) {$\vec{E}$} \node[blue,right] at (0.59,0.2) {$\vec{H}$} \node[right] at (0.32,0.32) {$\otimes\vec{S}$} \node[above] at (0.72,0) {$\otimes\vec{S}$} \node[right] at (0.32,-0.3) {$\otimes\vec{S}$} \node[right] at (-0.48,0.32) {$\odot\vec{S}$} \node[above] at (-0.72,0) {$\odot\vec{S}$} \node[right] at (-0.48,-0.3) {$\odot\vec{S}$} \draw [-{Latex}, blue] (0,0) -- (0,.15) node [right] {$\vec{\mathfrak{m}}$}; \begin{scope}[scale=0.3,on background layer] \foreach \a [count=\b] in {1.2}{ \draw[blue,domain=0:6.28,samples=150, line width=0.1mm, decoration={markings,% mark=at position 0.1 with {\arrowreversed{Stealth}}, mark=at position 0.4 with {\arrow{Stealth}}, mark=at position 0.5 with {\arrow{Stealth}}, mark=at position 0.6 with {\arrow{Stealth}}, mark=at position 0.9 with {\arrowreversed{Stealth}}, mark=at position 1 with {\arrowreversed{Stealth}},}, postaction=decorate] plot (xy polar cs:angle=\x r,radius={\a+\b*cos(2*\x r)}); } \end{scope} \end{tikzpicture}$$

Вектор Поинтинга есть

$$\vec{S} = {c\over 4\pi}\vec{E}\times\vec{H}.$$(2)

Он связан с плотностью импульса

$$\vec{P} = {\vec{S} \over c^2}.$$(3)

Тогда, собирая вместе, получаем

$$\vec{P} = {1\over 4\pi c}{Q \over R^2} {1 \over R^3}\left[ \vec{n}\times \left(3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n}) -\vec{\mathfrak{m}} \right) \right] = {Q\over 4\pi c R^5}\left[\vec{\mathfrak{m}} \times \vec{n}\right].$$

Момент импульса

$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV=\int\! R\,{Q\over 4\pi c R^5}\,\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]dV.$$(4)

Введем сферические координаты так, что $$\vec{\mathfrak{m}}$$ направлен вдоль оси z, а угол θ есть угол между осью z и направлением $$\vec{R}$$. Тогда

$$\vec{L}=\int\limits_a^{\infty}\!{Q\over 4\pi c R^4}R^2dR \int\!\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]d(\cos \theta)\,d\varphi.$$(5)

Первый интеграл берется элементарно. Второй есть усреднение двойного векторного произведения по всем направлениям $$\vec{n}$$, он кроме как от $$\vec{\mathfrak{m}}$$ ни от чего не зависит. Учитывая линейность интегрирования и векторного произведения, зависимость должна быть прямой пропорциональностью. Действительно, вычисления показывают, что второй интеграл равен

$$\vec{\mathfrak{m}}\int\!\sin^2\theta\,d(\cos \theta)\,d\varphi={8\pi\vec{\mathfrak{m}}\over 3}.$$

Окончательно получаем

$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$

Теперь посмотрим, какой момент импульса будет передан сфере после исчезновения магнитного поля. Начнем с момента электрических сил

$$\vec{M}=\int\!\vec{R}\times\rho\vec{E}\,dV={Q\over 4\pi}\int\!\vec{R}\times\vec{E}\,d(\cos\theta)\,d\varphi.$$

Учитывая, что вихревое электрическое поле определяется формулой

$$\vec{E}=-{1\over c}{\partial \vec{A}\over\partial t},$$

для момента импульса имеем

$$\vec{L}=\int\!\vec{M}\,dt={Q\over 4\pi c}\int\!d(\cos\theta)\,d\varphi\,\vec{R}\times\!\int\!-{\partial \vec{A}\over\partial t}dt.$$

Векторный потенциал уменьшается от начального значения $$\vec{A}$$, задаваемого формулой (1), до нуля. Поэтому последний интеграл просто равен $$\vec{A}$$. Таким образом,

$$\vec{L}=\cfrac{Q}{4\pi c a}\int\!d(\cos\theta)\,d\varphi\,\vec{n}\times \left[\vec{\mathfrak{m}} \times \vec{n}\right].$$

Это выражение совпадает с (5).

Как и ожидалось, весь момент импульса, запасенный в постоянном электромагнитном поле, передается зарядам при исчезновении магнитного поля.

← сюда туда →