Поиски бозона Хиггса на LHC
Сегодня в ЦЕРНе состоялся доклад коллабораций ATLAS и CMS, на котором были представлены предварительные результаты обработки данных, набранных в 2011 году. CMS уже исключил хиггсовский бозон стандартной модели в диапазоне масс от 128 до 600 ГэВ. С учетом ограничений, полученных на LEP, разрешенным является диапазон от 115 до 128 ГэВ. Он сейчас не закрыт
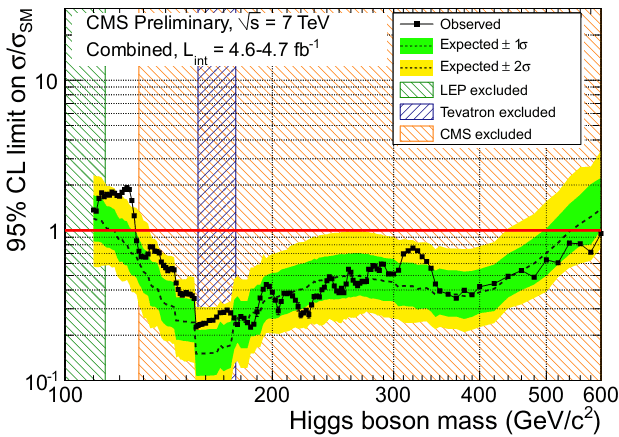
Именно там, на энергии в 126 ГэВ, ATLAS наблюдает пик в одном из возможных каналов распада (локально 3,6σ, глобально 2,3σ).
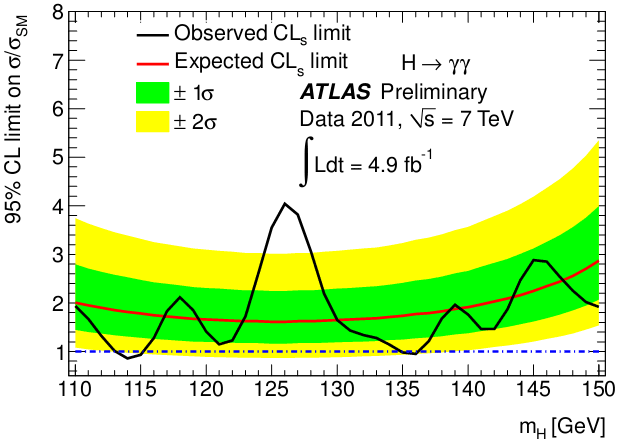
Если бозон Хиггса действительно существует, он должен проявляться в данных именно так. Но в то же время подобное превышение может оказаться случайным выбросом фоновых событий. Для полноценного открытия нужно превышение сигнала над ошибками в 5σ.
Доклад завершился словами о том, что хиггсовский бозон пока и не открыт, и не исключен.