Гравитация в пространстве (2+1)

Мы рассмотрим некоторые особенности гравитации в трехмерном пространстве-времени (две пространственных координаты плюс время). Оказывается, такое пространство в присутствии масс локально не искривляется, однако в нем появляются глобальные топологические эффекты. Например, длина окружности, охватывающей материальную точку, меньше, чем 2πR.

Тензор Римана в (2+1)

Как известно, тензор Римана обладает следующими симметриями:

$$R_{abcd}=R_{cdab},\quad R_{abcd}=-R_{bacd}=-R_{abdc},$$

где каждый индекс пробегает значения 0, 1, 2. Непосредственным перебором легко проверить, что у тензора Римана остается 6 независимых ненулевых компонент: R₀₁₀₁, R₀₁₁₂, R₀₁₂₀, R₁₂₁₂, R₁₂₂₀, R₂₀₂₀. Число независимых компонент тензора Риччи тоже 6. Оказывается, в трехмерном пространстве-времени тензор Римана можно выразить через тензор Риччи:

$$R_{abcd}=g_{ac}Q_{bd} + g_{bd}Q_{ac}-g_{ad}Q_{bc}-g_{bc}Q_{ad},$$(1)

где Q_ab ≡ R_ab − ¼g_abR, R ≡ R^a_a.

Точечная масса

Вычислим статическую аксиально-симметричную метрику в присутствии точечной массы. Как обычно, начинаем с уравнений Эйнштейна

$$R_{ab} -{R \over 2} g_{ab} = {8 \pi G \over c^4} T_{ab}.$$

Взяв след обеих частей, получаем

$$R = -{16 \pi G \over c^4} T.$$(2)

В пустом пространстве вокруг тела T_ab ≡ 0, следовательно, из (2), уравнения Эйнштейна и (1) получаем R ≡ 0, R_ab ≡ 0, R_abcd ≡ 0. Таким образом, пустое пространство (2+1) должно быть локально плоским. Это, в частности, означает, что в рассматриваемом случае нет гравитационных волн.

Метрика такого пространства с учетом симметрий имеет следующий вид:

$$ds^2=-c^2dt^2+d\rho^2+\alpha^2\rho^2d\varphi^2,$$

где $$\alpha^2$$ — некоторая константа, а φ меняется от 0 до 2π. Введем новую угловую координату φ′ = αφ. Константа α и будет определять глобальные гравитационные эффекты. Заглядывая вперед, скажем, что α < 1. Таким образом, длина окружности, охватывающей точечную массу, будет меньше, чем 2πR.

Время входит в интервал с постоянным коэффициентом и не смешивается с другими координатами, поэтому скаляр кривизны R определяется только пространственной частью метрики.

Конический дефект

Двумерное пространство, описываемое такой метрикой, соответствует конической поверхности. В каждой точке поверхности, за исключением вершины, тензор Риччи равен нулю. В вершине имеется расходимость, связанная с расходимостью плотности энергии точечного тела.

Обычно связь между массой (которая пропорциональна коэффициенту в кривизне, задаваемой дельта-функцией) и величиной дефекта α определяется через эйлерову характеристику поверхности (которая равна сумме интеграла от кривизны по поверхности и интеграла от «внешней кривизны» границы по самой границе). Мы же пойдем более наглядным и методически более простым путем, «размывая» точечную массу.

Можно было бы рассмотреть некоторое распределение массы в ограниченной области и выяснить, как будет меняться α, когда размер области стремится к нулю. Однако мы будем действовать противоположным образом, что избавит нас от необходимости решать уравнения Эйнштейна. Деформируем коническую поверхность, «сгладив» вершину в сферический сегмент радиуса r, и выясним, какому распределению масс соответствует такое пространство.

Известно, что скаляр кривизны двумерной поверхности равен удвоенной гауссовой кривизне:

$$R = {2 K} = {2 \over r_1r_2},$$

где r₁ и r₂ — главные радиусы кривизны поверхности. Для сферической поверхности радиуса r скаляр кривизны R = 2/r².

Установим некоторые геометрические соотношения. Длина окружности в основании конуса равна $$2\pi|AB|=2\pi\rho\sin\beta$$, длина той же линии на развертке конуса равна $$2\pi\alpha|AP|=2\pi\alpha\rho$$, откуда $$\alpha=\sin\beta$$. Тогда площадь $$S=2\pi r\cdot |BC|$$ сферического сегмента высоты $$|BC|=h=r(1-\sin\beta)$$ выражается как $$2\pi r^2(1-\alpha)$$.

Проинтегрируем (2):

$$\int T \sqrt{-g}\, d^2x =- {c^4 \over 16\pi G}\int R \sqrt{-g}\, d^2 x=-{c^4 \over 16\pi G}RS = -{c^4 \over 4G} (1- \alpha).$$

Учитывая аддитивность массы (отсутствие гравитационного дефекта массы следует из того, что тензор Римана в пустом пространстве нулевой и пространство локально галилеево; мы обсудим это ниже), получаем

$$mc^2 =\int {T_{00}} \sqrt{-g}\, d^2x=-\int T \sqrt{-g}\, d^2x={c^4 \over 4G} (1-\alpha) ,$$

$$\alpha =1-{4Gm \over c^2}.$$

Интеграл от скаляра кривизны по поверхности не зависит от размера области «сглаживания», поэтому полученный результат справедлив и для точечной массы, когда r → 0. Как видим, для обычных тел с положительной массой α < 1. Видно также, что масса рассматриваемого тела не может превышать величину c²/4G.

Геодезические

Решая систему уравнений для геодезических

$$\frac{d^2x^\lambda }{d s^2} + \Gamma^{\lambda}_{~\mu \nu }\frac{dx^\mu }{d s}\frac{dx^\nu }{d s} = 0,$$

которая в наших координатах принимает вид

$$\left\{ \begin{array}{l}\ddot{\varphi} + \dfrac{2}{r}\dot{r}\dot{\varphi}=0, \\ \ddot{r}-r\dot{\varphi}^2\alpha^2=0, \\ \end{array} \right. $$

легко убедиться в том, что геодезические для пространства с точечной массой — это прямые $$r\sim 1/\sin(\alpha\varphi)$$ на развертке конуса.

Можно спроецировать геодезические на плоскость, перпендикулярную оси конуса. Тогда получится, что точечная масса «искривляет» пространство, или «отклоняет» движущиеся частицы. Однако легко видеть, что угол «отклонения» не зависит от прицельного параметра. Таким образом, уравнения Эйнштейна в (2+1) не содержат ньютоновское тяготение как предельный случай.

Более того, как показывает изучение геодезических, в определенном смысле гравитационное взаимодействие в (2+1) отсутствует. Как видно из вышеприведенной системы, для любых r₀ и φ₀ «кривая» покоя r = r₀, φ = φ₀ является геодезической. В обычном четырехмерном случае это не так. Например, для шварцшильдовского решения не существует такой системы координат, в которой тело в любой точке оставалось бы в покое.

Обобщения

Мы убедились в том, что точечной массе в трехмерном пространстве-времени соответствует плоскость с вырезанным углом (в вершине которого сама материальная точка) и отождествленными точками на противоположных сторонах разреза. Подобная картина характерна и для нескольких точек. С каждым телом связан вырезанный угол, величина которого пропорциональна массе тела. Сумма масс всех тел также не может превышать c²/4G.

Помимо бесконечной двумерной поверхности, можно представить еще и замкнутую поверхность, топологически эквивалентную сфере. Очевидно, масса такой замкнутой Вселенной есть c²/2G. Сфера будет реализовываться в случае равномерного распределения вещества. Дискретные массы будут образовывать многогранники. Например, восемь одинаковых материальных точек могут дать куб.

Ультрабуст в пространстве (2+1)

В прошлый раз, говоря о (2+1)-мерной гравитации, мы нашли метрику точечной массы:

$$ds^2=-c^2dt^2+d\rho^2+\alpha^2\rho^2d\varphi^2,\quad\alpha=1-4Gm/c^2.$$(1)

Теперь попробуем вывести метрику ультрарелятивистской частицы, пролетающей мимо наблюдателя с околосветовой скоростью. Сначала мы найдем метрику движущейся материальной точки, а затем применим операцию, называемую ультрабустом. Она заключается в одновременном устремлении скорости частицы к скорости света и массы к нулю, чтобы энергия оставалась конечной.

Лоренцев буст

Временно будем считать, что скорость света с = 1.

Для плоской метрики пространства Минковского переход в другую ИСО выполняется при помощи матрицы Лоренца Λ (такое преобразование оставляет метрику инвариантной):

$$g(v)=\Lambda^Tg\Lambda.$$(2)

Эту формулу можно применять не только к плоскому пространству, но и, например, к решению Шварцшильда. Действительно, метрика Шварцшильда асимптотически плоская, поэтому, формально проделав над ней такое преобразование, мы получим на бесконечности преобразования Лоренца из СТО. Следовательно, (2) описывает переход из системы отсчета покоя в систему, движущуюся относительно тела с постоянной скоростью.

Однако метрика (1) не является асимптотически плоской, поэтому обоснование возможности применить (2) в случае пространства (2+1) сложнее.

Для начала заменим переменные:

$$\left\{ \begin{array}{rl} x\!\!\!\!&=r\cos\varphi,\\ y\!\!\!\!&=r\sin\varphi,\\ \varepsilon\!\!\!\!&=1-\alpha^2. \end{array} $$(3)

В этих обозначениях метрика (1) принимает вид

$$g=\left[ \begin{array}{ccc} -1&0&0 \\ 0&1-{\dfrac {\varepsilon\,{y}^{2}}{{x}^{2}+{y}^{2}}}&{\dfrac {\varepsilon\,xy}{{x}^{2}+{y}^{2}}} \\ 0&{\dfrac {\varepsilon\,xy}{{x}^{2}+{y}^{2}}}&1-{\dfrac {\varepsilon\,{x}^{2}}{{x}^{2}+{y}^{2}}} \end{array} \right] .$$

Отсюда и из (1) видно, что ε → 0, когда m → 0. Когда мы уменьшаем массу точки до нуля, пространство переходит в плоское. Результат цепочки преобразований: уменьшение массы до нуля — лоренцев буст — увеличение массы до первоначального значения совпадет с результатом от простого применения формулы (2). Этим и обосновывается возможность ее применения.

Матрица Лоренца есть

$$\Lambda=\left[ \begin {array}{ccc} {\cfrac {1}{\sqrt {1-v^{2}}}}&-{\cfrac {v}{\sqrt {1-v^{2}}}}&0 \\ -{\cfrac{v}{\sqrt {1-{v}^{2}}}}&{\cfrac {1}{\sqrt {1-v^{2}}}}&0 \\ 0&0&1\end {array} \right] .$$

Несложные, но объемные вычисления, которые лучше всего поручить компьютеру, дают

$$\Lambda^Tg\Lambda=\left[\begin{array}{ccc} -1-{v^2\over 1-v^2}{\varepsilon y^2\over x^2+y^2}&{v\over 1-v^2}{\varepsilon y^2\over x^2+y^2}&-{v\over\sqrt{1-v^2}}{\varepsilon xy \over x^2+y^2}}\\ \noalign{\medskip}{v\over 1-v^2}{\varepsilon y^2\over x^2+y^2}&1-{1\over 1-v^2}{\varepsilon y^2\over x^2+y^2}&{1\over\sqrt{1-v^2}}{\varepsilon xy \over x^2+y^2}}\\ \noalign{\medskip}-{v\over\sqrt{1-v^2}}{\varepsilon xy \over x^2+y^2}}&{1\over\sqrt{1-v^2}}{\varepsilon xy \over x^2+y^2}}&1-{\varepsilon x^2 \over x^2+y^2}\end {array}\right].$$

В этом выражении x — координата в сопутствующей системе отсчета. Она связана с координатой x₁ в нашей системе отсчета преобразованием Лоренца

$$x = {x_1-vt \over \sqrt{1-v^2}}.$$

Подставим ее в предыдущее выражение и получим

$$g(v)=\left[\begin{array}{ccc}-1-{v^2\varepsilon y^2\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}&{v\varepsilon y^2\over\left(x_1-vt\right)^2+y^2\left( 1-v^2 \right)}&-{v\varepsilon\left(x_1-vt\right)y\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}\\ \noalign{\medskip}{v\varepsilon y^2\over \left(x_1-vt\right)^2+y^2\left( 1-v^2 \right)}&1-{\varepsilon y^2\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}&{\varepsilon\left( x_1-vt\right)y\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}\\ \noalign{\medskip}-{v\varepsilon\left( x_1-vt \right) y\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}&{\varepsilon\left(x_1-vt\right)y\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}&1-{\varepsilon\left(x_1-vt\right)^2\over\left(x_1-vt\right)^2+y^2\left(1-v^2\right)}\end{array}\right].$$

Ультрабуст

Используем результат, полученный выше, для вывода метрики материальной точки с нулевой массой, движущейся со скоростью света.

Будем переходить к пределу v → c, m → 0 таким образом, чтобы энергия

$$E={mc^2 \over \sqrt{1-\dfrac{v^2}{c^2}}}$$

материальной точки оставалась конечной. С учетом (1) и (3) легко найти, что

$$\varepsilon={8GE \over {c^4}}\sqrt {1-\dfrac{v^2}{c^2}}-{16G^2E^2 \over c^8}\left( {1-\dfrac{v^2}{c^2}} \right).$$

Кроме того, нам понадобится известное соотношение

$$\lim \limits_{a\to +0} \dfrac{a}{z^2+a^2}=\pi \delta (z).$$

В конечном итоге мы получим

$$g(c ) =\left[\begin{array}{ccc} {-c^2-\dfrac{8\pi G}{c^2}E\left| y \right|\delta \left( {x_1 -ct} \right)}& {\dfrac{8\pi G}{c^3}E\left| y \right|\delta \left( {x_1 -ct} \right)}& 0\\{\dfrac{8\pi G}{c^3}E\left| y \right|\delta \left( {x_1 -ct} \right)}& {1-\dfrac{8\pi G}{c^4}E\left| y \right|\delta \left( {x_1 -ct} \right)}& 0 \\ 0& 0& 1\\ \end{array}\right] .$$

В переменных u = x₁ − ct, v = x₁ + ct интервал принимает вид

$$ds^2=-du\,dv+dy^2-\dfrac{8\pi G}{c^4}E\,\delta (u) \left| y \right|du^2.$$

Полезно сравнить этот ответ с ультрабустом в (3+1) [1]:

$$ds^2=-du\,dv+dr^2+r^2 d\theta ^2-8GE\,\delta (u) \ln r du^2.$$

Результаты отличаются функцией от перпендикулярного расстояния, входящей в коэффициент перед du². В двумерном случае это линейная функция, а в трехмерном — логарифм. Эти функции являются функциями Грина уравнения Лапласа размерности на 2 меньше, чем размерность соответствующего пространства-времени. Как видим, результаты получились похожими.

Ссылки

[1] P. C. Aichelburg, R. U. Sexl (Vienna U.). «On the Gravitational field of a massless particle». May 1970. Published in Gen.Rel.Grav.2:303-312,1971.

[2] S. Deser, Alan R. Steif (Brandeis U.). «Gravity theories with lightlike sources in D = 3.» Published in Class.Quant.Grav.9:L153-L160,1992.

Парадокс Фейнмана, или потоки энергии в постоянных электромагнитных полях

В фейнмановских лекциях по физике (выпуск 6, глава 17) есть описание следующего парадокса.

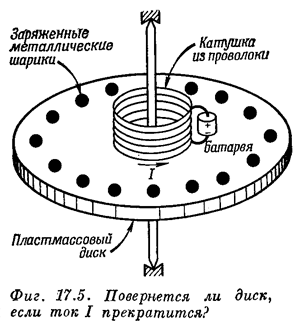
Представим, что мы конструируем прибор, в котором имеется тонкий круглый пластмассовый диск, укрепленный концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается. На диске имеется катушка из проволоки — короткий соленоид, концентричный по отношению к оси вращения. Через этот соленоид проходит постоянный ток I от маленькой батареи, также укрепленной на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одинаковым зарядом Q. Вся картина стационарна, и диск неподвижен.

Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без какого-либо вмешательства извне. Пока через соленоид шел ток, более или менее параллельно оси диска проходил магнитный поток. После того как ток прервался, поток этот должен уменьшиться до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружностям с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внешней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вращающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнет вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую скорость.

Но можно рассуждать и по-другому. Используя закон сохранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нулевым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернется ли диск или нет? Мы предлагаем вам подумать над этим вопросом.

Решение парадокса заключается в том, что в присутствии электрических и магнитных полей имеются потоки энергии, описываемые вектором Пойнтинга $$\vec{S} \sim \vec{E} \times \vec{B}$$. В предложенной Фейнманом конфигурации эти потоки замкнуты. Поскольку поток энергии однозначно связан с плотностью импульса, наличие замкнутых потоков энергии свидетельствует о присутствии ненулевого момента импульса. Таким образом, в системе изначально был запас момента импульса, который после исчезновения магнитного поля был передан диску.

Однако есть люди, которые убеждены в том, что выражение для вектора потока энергии через векторное произведение полей годится только для переменных электромагнитных полей (действительно, перенос энергии в этом случае можно увидеть непосредственно). Им не нравится, что, согласно выражению для вектора Пойнтинга, энергия течет от источника постоянного тока к нагрузке не «по проводам», а снаружи. Основной аргумент сводится к тому, что на поток энергии легко влияют манипуляции с проводом, наличие примесей, разрывов; в то время как никакими телами снаружи, например, дополнительными зарядами или магнитами, остановить поток энергии к нагрузке не удается.

Противники применения вектора Пойнтинга в статике придумывают в этом случае другие выражения для плотности энергии, например, $$\varphi \vec{j}$$. Но такое выражение тоже не лишено недостатков, приписываемых вектору Пойнтинга. Даже если отбросить требование единообразного описания явлений и попытаться применить для зарядов и катушки выражение $$\varphi \vec{j}$$, мы сразу столкнемся с тем, что потенциал φ в точках катушки (а, значит, и и момент импульса системы) легко изменить, поместив систему внутрь большого проводящего заряженного ящика и меняя его заряд. Это плохо согласуется с гипотезой, по которой энергия, как и ток, течет по катушке.

В связи с такой критикой вектора Пойнтинга можно заняться интересным упражнением — непосредственно вычислить момент импульса электромагнитного поля через вектор Пойнтинга и сравнить его с моментом импульса, передаваемым диску. Даже если критиков эти вычисления не убедят, мы еще раз увидим красоту теории.

$$\begin{tikzpicture}[x=(-30:3cm),y=(30:3cm),z=(90:3cm),>=stealth] \def\R{1} \draw[blue,->] (0,0,0) -- (0,0,0.3\R) node[right] {$\vec{\mathfrak{m}}$}; \draw[thin] (0,0,0) -- (.7\R,.7\R,0) node[below,pos=0.5] {$a$}; \node[orange!80!black] at (0,\R,0.5*\R) {$Q$}; \def\r{0.075} \draw[blue,->,thick] (\r,0,0) arc (0:360:\r); \foreach \i in {0, 30,...,150} \draw [orange!40!black,dotted] plot [domain=-180:180, samples=30, variable=\j] (\R*cos \i*sin \j,\R*sin \i*sin \j, \R*cos \j); \foreach \j in {0, 15,...,165} \draw [orange!40!black,dotted] plot [domain=0:360, samples=60, variable=\i] (\R*cos \i*sin \j,\R*sin \i*sin \j, \R*cos \j); \end{tikzpicture}$$

Для упрощения вычислений изменим систему, предложенную Фейнманом. Будем рассматривать не заряды на краю диска, а равномерно заряженную сферу радиуса a, в центре которой находится небольшая катушка, обладающая магнитным моментом $$\vec{\mathfrak{m}}$$. Магнитный момент, находящийся в начале координат, создает в точке $$\vec{R}$$ векторный потенциал

$$\vec{A} = {\vec{\mathfrak{m}} \times \vec{R} \over R^3}$$(1)

и магнитное поле

$$\vec{H} = {3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n})-\vec{\mathfrak{m}} \over R^3}, \quad \vec{n} = {\vec{R}\over R}.$$

$$\usetikzlibrary{arrows.meta,positioning,decorations.markings,backgrounds} \colorlet{EcolFL}{orange!80!black} \tikzset{EFieldLineArrow/.style={EcolFL,decoration={markings,mark=at position 1 with {\arrow{Stealth}}},postaction={decorate}}} \def\R{0.8} \def\NE{8} \begin{tikzpicture}[-,scale=6] \foreach \i [evaluate={\angle=(\i-1)*360/\NE;}] in {1,...,\NE}{ \draw[EFieldLineArrow] (\angle:0) -- (\angle:\R); } \node[draw=EcolFL,fill=white,circle, minimum size=4cm, inner sep=0, outer sep=0] (circ) at (0,0) {}; \node[EcolFL,right] at (0.56,0.56) {$\vec{E}$} \node[blue,right] at (0.59,0.2) {$\vec{H}$} \node[right] at (0.32,0.32) {$\otimes\vec{S}$} \node[above] at (0.72,0) {$\otimes\vec{S}$} \node[right] at (0.32,-0.3) {$\otimes\vec{S}$} \node[right] at (-0.48,0.32) {$\odot\vec{S}$} \node[above] at (-0.72,0) {$\odot\vec{S}$} \node[right] at (-0.48,-0.3) {$\odot\vec{S}$} \draw [-{Latex}, blue] (0,0) -- (0,.15) node [right] {$\vec{\mathfrak{m}}$}; \begin{scope}[scale=0.3,on background layer] \foreach \a [count=\b] in {1.2}{ \draw[blue,domain=0:6.28,samples=150, line width=0.1mm, decoration={markings,% mark=at position 0.1 with {\arrowreversed{Stealth}}, mark=at position 0.4 with {\arrow{Stealth}}, mark=at position 0.5 with {\arrow{Stealth}}, mark=at position 0.6 with {\arrow{Stealth}}, mark=at position 0.9 with {\arrowreversed{Stealth}}, mark=at position 1 with {\arrowreversed{Stealth}},}, postaction=decorate] plot (xy polar cs:angle=\x r,radius={\a+\b*cos(2*\x r)}); } \end{scope} \end{tikzpicture}$$

Вектор Поинтинга есть

$$\vec{S} = {c\over 4\pi}\vec{E}\times\vec{H}.$$(2)

Он связан с плотностью импульса

$$\vec{P} = {\vec{S} \over c^2}.$$(3)

Тогда, собирая вместе, получаем

$$\vec{P} = {1\over 4\pi c}{Q \over R^2} {1 \over R^3}\left[ \vec{n}\times \left(3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n}) -\vec{\mathfrak{m}} \right) \right] = {Q\over 4\pi c R^5}\left[\vec{\mathfrak{m}} \times \vec{n}\right].$$

Момент импульса

$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV=\int\! R\,{Q\over 4\pi c R^5}\,\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]dV.$$(4)

Введем сферические координаты так, что $$\vec{\mathfrak{m}}$$ направлен вдоль оси z, а угол θ есть угол между осью z и направлением $$\vec{R}$$. Тогда

$$\vec{L}=\int\limits_a^{\infty}\!{Q\over 4\pi c R^4}R^2dR \int\!\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]d(\cos \theta)\,d\varphi.$$(5)

Первый интеграл берется элементарно. Второй есть усреднение двойного векторного произведения по всем направлениям $$\vec{n}$$, он кроме как от $$\vec{\mathfrak{m}}$$ ни от чего не зависит. Учитывая линейность интегрирования и векторного произведения, зависимость должна быть прямой пропорциональностью. Действительно, вычисления показывают, что второй интеграл равен

$$\vec{\mathfrak{m}}\int\!\sin^2\theta\,d(\cos \theta)\,d\varphi={8\pi\vec{\mathfrak{m}}\over 3}.$$

Окончательно получаем

$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$

Теперь посмотрим, какой момент импульса будет передан сфере после исчезновения магнитного поля. Начнем с момента электрических сил

$$\vec{M}=\int\!\vec{R}\times\rho\vec{E}\,dV={Q\over 4\pi}\int\!\vec{R}\times\vec{E}\,d(\cos\theta)\,d\varphi.$$

Учитывая, что вихревое электрическое поле определяется формулой

$$\vec{E}=-{1\over c}{\partial \vec{A}\over\partial t},$$

для момента импульса имеем

$$\vec{L}=\int\!\vec{M}\,dt={Q\over 4\pi c}\int\!d(\cos\theta)\,d\varphi\,\vec{R}\times\!\int\!-{\partial \vec{A}\over\partial t}dt.$$

Векторный потенциал уменьшается от начального значения $$\vec{A}$$, задаваемого формулой (1), до нуля. Поэтому последний интеграл просто равен $$\vec{A}$$. Таким образом,

$$\vec{L}=\cfrac{Q}{4\pi c a}\int\!d(\cos\theta)\,d\varphi\,\vec{n}\times \left[\vec{\mathfrak{m}} \times \vec{n}\right].$$

Это выражение совпадает с (5).

Как и ожидалось, весь момент импульса, запасенный в постоянном электромагнитном поле, передается зарядам при исчезновении магнитного поля.

Простейшая модель электрона: электромагнитная масса и гиромагнитное отношение

Продолжим развлекаться с классической электродинамикой. В прошлый раз мы подсчитали момент импульса в системе, состоящей из магнитного момента (маленькой катушки) в центре большой равномерно заряженной сферы

$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$(1)

Но магнитное поле вокруг сферы можно создать без дополнительной катушки, просто закрутив ее. Получается, что часть момента импульса вращающейся сферы запасается в ее электромагнитном поле. Определим эту добавку.

Магнитный момент вращающейся сферы 

Мы собираемся показать, что магнитное поле вне равномерно заряженной сферы радиуса a и заряда Q, вращающейся с угловой скоростью ω, точно совпадает с полем магнитного диполя.

Начинаем с векторного потенциала

$$\vec{A}={1\over c}\int\!{\vec{j}\over r}\,dV={Q\over 4\pi ca^2}\int\!{\vec{v}\over r}\,dS={Q\over 4\pi ca^2}\int\!{\vec{\omega}\times a\vec{n}\over r}\,dS,$$

где $$r=|\vec{R}-a\vec{n}|$$ — расстояние от элемента поверхности dS, задаваемого радиус-вектором $$a\vec{n}$$, до точки $$\vec{R}$$, в которой вычисляется векторный потенциал. Учитывая линейность векторного произведения, получаем

$$\vec{A}={Q\over 4\pi ca}\,\vec{\omega}\times\int\!{\vec{n}\over \sqrt{R^2 + a^2-2Ra\cos\chi}}\,dS={Q\over 4\pi ca}\,\vec{\omega}\times\vec{I}.$$

Интеграл $$\vec{I}$$ в последнем выражении — это усреднение единичного вектора $$\vec{n}$$ по направлениям с весом 1/r. Исходя из соображений симметрии ясно, что в результате интегрирования мы получим вектор, параллельный вектору $$\vec{R}$$. Подтвердим это вычислением.

В сферических координатах $$\inline \vec{n}=(\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)$$. Направим вектор $$\vec{R}=(0,0,R)$$ вдоль оси z. Тогда угол χ между векторами $$\inline \vec{n}$$ и $$\inline \vec{R}$$ совпадает со сферической координатой θ. Z-компонента интеграла

$$I_z=a^2\int\!\cos\theta\,{1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}\,d(\cos\theta)\,d\varphi.$$

Известно, что функцию 1/r можно разложить по многочленам Лежандра (нас интересует область R > a)

$${1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}=\sum\limits_{l=0}^\infty{a^l\over R^{l+1}}P_l(\cos\theta).$$

Подынтегральное выражение состоит из произведения этого ряда на многочлен Лежандра $$P_1(\cos\theta)=\cos\theta$$. Тогда из условия ортогональности

$$\int\limits_{-1}^{1} P_k(x)P_l(x)\,dx={2\over 2k+1}\delta_{kl}$$

сразу следует ответ

$$I_z={4\pi\over 3}{a^3\over R^2}.$$

Компоненты I_x и I_y пропорциональны интегралам от периодических функций sin φ и cos φ, и поэтому равны нулю. Переходя от проекций к вектору, для векторного потенциала получаем

$$\vec{A}={Qa^2\over 3c}\,\vec{\omega}\times{\vec{R}\over R^3}.$$

Таким образом, магнитное поле вне вращающейся сферы совпадает с полем магнитного диполя

$$\vec{\mathfrak{m}}={Qa^2\vec{\omega}\over 3c}.$$(2)

Для полноты отметим, что аналогичными вычислениями легко показать однородность магнитного поля внутри вращающейся сферы.

Электромагнитная масса

Коэффициент в (1) можно переписать по-другому, если ввести понятие электромагнитной массы. Оно подробно разбирается в главе 28 выпуска 6 фейнмановских лекций (ниже мы воспроизводим некоторые вычисления оттуда и фактически на протяжении двух постов разбираем задачу 2 к этой главе).

Вслед за Фейнманом мы будем называть электромагнитной массой коэффициент пропорциональности между скоростью равномерного движения сферы и импульсом электромагнитного поля. В нерелятивистском случае

$$\vec{E}=Q{\vec{R}\over R^3},\quad\vec{H}={Q\over c}{\vec{v}\times\vec{R}\over R^3}.$$

Тогда импульс электромагнитного поля дается интегралом

$$\vec{P}={1\over 4\pi c}\int\!\vec{E}\times\vec{H}\,dV={Q^2\over 4\pi c^2}\int\!{1\over R^4}\,\vec{n}\times\left[\vec{v}\times\vec{n}\right]\,dV.$$

Такой интеграл (с точностью до коэффициента) мы вычисляли в прошлый раз, поэтому сейчас просто выпишем ответ

$$\vec{P}={2Q^2 \over 3 ac^2}\,\vec{v}=m_e \vec{v}.$$

Гиромагнитное отношение и модель электрона

Теперь мы можем переписать (1) в таком виде

$$\vec{L}={m_ec\over Q}\,\vec{\mathfrak{m}}.$$

Мы получили интересный результат: гиромагнитное отношение для вращающейся безмассовой заряженной сферы совпадает с гиромагнитным отношением электрона.

Обычно в литературе по квантовой механике утверждается, что нельзя представлять себе спин электрона как его вращение, так как в такой модели скорость точек на его поверхности будет больше скорости света. Сейчас мы в этом убедимся.

Подставим в (1) магнитный момент (2) и спин электрона ½:

$${\hbar\over 2}={2\over 3}\,{Q\over ca}\,{Qa^2\omega\over 3c},$$

откуда отношение экваториальной скорости к скорости света есть

$${a\omega\over c}={9\over 4}\,{\hbar c\over Q^2}={9\over 4\alpha}\approx308.$$

Несостоятельность простейшей модели электрона проявляется и в том, что полная энергия электрического поля

$$U={1\over 8\pi}\int\!{E^2}\,dV={1\over 8\pi}\int\limits_a^{\infty}{Q^2\over R^4}\,4\pi R^2\,dR={Q^2 \over 2a}={4\over 3}\,m_ec^2$$

отличается от ожидаемой величины m_ec².

← сюда туда →